G15: Modellieren - Anwenden von quadratischen Gleichungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Zunächst sind diese Schritte zu befolgen: 1)Aufstellung der Gleichung 2)Umformen zur pq-Formel 3)Lösen der pq-Formel 4)Probe 5)Antwortsatz Beispiel: Die Quadr...) |
|||
| Zeile 18: | Zeile 18: | ||
[[Bild:Bild.jpg]] | [[Bild:Bild.jpg]] | ||
| − | 1)(5-X)(5-X)=17.62 | + | 1)x²+(5-X)(5-X)=17.62 |
Erläuterung: Man nimmt5-X, weil die Seitenlänge 5cm beträgt und wir aber nur den Flächeninhalt des größeren Quadrates berechnen wollen.Also rechnen wir -X,sprich:- Die Seite des kleinen Quadrates.Wir multiplizieren es mit 5-X, weil die andere Seitenlänge ebenso viel beträgt. | Erläuterung: Man nimmt5-X, weil die Seitenlänge 5cm beträgt und wir aber nur den Flächeninhalt des größeren Quadrates berechnen wollen.Also rechnen wir -X,sprich:- Die Seite des kleinen Quadrates.Wir multiplizieren es mit 5-X, weil die andere Seitenlänge ebenso viel beträgt. | ||
| − | 2)Jetzt wird die Gleichung nach Null aufgelöst: 25-5X-5X + | + | 2)Jetzt wird die Gleichung nach Null aufgelöst: 25-5X-5X +2x²=17.62 I-17.62 |
| − | = | + | = 2x²-10x +7.38=0 I :2 |
| + | = x²-5x+3,69=0 | ||
| + | 3)Jetzt lösen wir die Pq-Formel auf: | ||
| + | x²-5x+3,69=0 | ||
| + | X1/2=2,5+<math>2,5²-3,69</math> | ||
| + | - | ||
| + | = 2,5²+<math>6,25-3,69</math> | ||
| + | - | ||
| + | = 2,5+<math>2,56</math> | ||
| + | - | ||
| + | = 2.5+1,6 | ||
| + | - | ||
| + | |||
| + | x1= 4,1 x2=0,9 | ||
| − | + | 4) Probe: Hierzu nehmen wir die Ausgangsgleichung, und setzen die x dafür ein: | |
| − | + | ||
| − | + | ||
| − | + | - | |
Version vom 18. Dezember 2009, 14:08 Uhr
Zunächst sind diese Schritte zu befolgen:
1)Aufstellung der Gleichung
2)Umformen zur pq-Formel
3)Lösen der pq-Formel
4)Probe
5)Antwortsatz
Beispiel:
Die Quadratseite ist 5cm lang. Die blaue Fläche hat den angegebenen Flächeninhalt.
Berechne die Seitenlänge X

1)x²+(5-X)(5-X)=17.62 Erläuterung: Man nimmt5-X, weil die Seitenlänge 5cm beträgt und wir aber nur den Flächeninhalt des größeren Quadrates berechnen wollen.Also rechnen wir -X,sprich:- Die Seite des kleinen Quadrates.Wir multiplizieren es mit 5-X, weil die andere Seitenlänge ebenso viel beträgt. 2)Jetzt wird die Gleichung nach Null aufgelöst: 25-5X-5X +2x²=17.62 I-17.62
= 2x²-10x +7.38=0 I :2
= x²-5x+3,69=0
3)Jetzt lösen wir die Pq-Formel auf:
x²-5x+3,69=0
X1/2=2,5+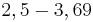 -
= 2,5²+
-
= 2,5²+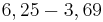 -
= 2,5+
-
= 2,5+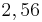 -
= 2.5+1,6
-
x1= 4,1 x2=0,9
-
= 2.5+1,6
-
x1= 4,1 x2=0,9
4) Probe: Hierzu nehmen wir die Ausgangsgleichung, und setzen die x dafür ein:
-

