G13: Lösen quadratischer Gleichungen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Aufstellen quadratischer Gleichungen= | + | =Aufstellen quadratischer Gleichungen= |
Um eine quadratische Gleichung zu lösen muss man erstmal eine Gleichung der Form | Um eine quadratische Gleichung zu lösen muss man erstmal eine Gleichung der Form | ||
| Zeile 20: | Zeile 20: | ||
Der nächste Schritt ist das Einsetzen in die Form. Wenn man nun die Gleichung nach x aufgelöst hat erhält man ein Ergebnis | Der nächste Schritt ist das Einsetzen in die Form. Wenn man nun die Gleichung nach x aufgelöst hat erhält man ein Ergebnis | ||
nach folgendem Schema: <br /> | nach folgendem Schema: <br /> | ||
| − | x<sub>1</sub> | + | x<sub>1</sub>=Ergebnis der Gleichung Nr.1 x<sub>2</sub>=Ergebnis der Gleichung Nr.2<br /> |
| + | Es gibt zwei Ergebnisse, da man aus einer Wurzel etwas negatives oder etwas postives ziehen kann.<br /> | ||
| + | |||
| + | =Probe= | ||
| + | Um herauszufinden ob das Ergebnis stimmt, kann man eine Probe durchführen. Diese geht folgendermaßen:<br /> | ||
| + | Man muss in die Ausgangsgleichung(siehe oben) Das ersteErgebinis für x einsetzen und die Gleichung dementsprechend nach x auflösen. | ||
| + | Kommt am Ende zum Beispiel 4=4 heraus weiß man dass das Ergebnis stimmt. Da es zwei Lösungen gibt, muss man die beiden | ||
| + | Ergebnisse getrennt voneinander in die Gleichung einsetzen und ausrechnen. | ||
| + | |||
| + | =Quellen und Hilfen im Internet= | ||
| + | Herr Beckers, unser Mathelehrer ;) <br /> | ||
| + | www.ardnt-bruenner.de/mathe/9/quadratischegleichungen.html<br /> | ||
| + | www.Mathepower.com/qgleich.php<br /> | ||
| + | www.lehrer-online.de/quadratische-funktionen-gleichungen.php<br /> | ||
| + | von Rachel Liven und Lukas F. | ||
Version vom 18. Dezember 2009, 14:12 Uhr
Inhaltsverzeichnis |
Aufstellen quadratischer Gleichungen
Um eine quadratische Gleichung zu lösen muss man erstmal eine Gleichung der Form
"x²+px+q=0" ,aufstellen.
Anschließend kann man die p-q-Formel anwenden um die Nullstellen der Parabel zu errechnen.
Beispiel:
x(x+5)=3 Dies ist die Ausgangssituation
x²+5x=3 Umformung mit Ausmultiplizieren
x³+5x-3=0 Die 3 auf die andere Seite gezogen - und man erhält eine passende Gleichung an der man die pq-Formel anwenden kann
Lösen quadratischer Gleichungen
Die pq-Formel erlaubt einem die Nullstellen einer Parabel auszurechnen ohne die Funktion der Parabel überhaupt zu kennen.
Man kann mit den Nullstellen außerdem noch die Ergebnisse von vielen praktischen Aufgaben herausfinden.
Um die pq-Formel anzuwenden braucht man zunächst eine Gleichung der Form "x²+px+q=0"
Diese Form verwandelt man dann in die pq-Formel:
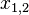 =
= 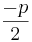
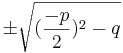
Der nächste Schritt ist das Einsetzen in die Form. Wenn man nun die Gleichung nach x aufgelöst hat erhält man ein Ergebnis
nach folgendem Schema:
x1=Ergebnis der Gleichung Nr.1 x2=Ergebnis der Gleichung Nr.2
Es gibt zwei Ergebnisse, da man aus einer Wurzel etwas negatives oder etwas postives ziehen kann.
Probe
Um herauszufinden ob das Ergebnis stimmt, kann man eine Probe durchführen. Diese geht folgendermaßen:
Man muss in die Ausgangsgleichung(siehe oben) Das ersteErgebinis für x einsetzen und die Gleichung dementsprechend nach x auflösen.
Kommt am Ende zum Beispiel 4=4 heraus weiß man dass das Ergebnis stimmt. Da es zwei Lösungen gibt, muss man die beiden
Ergebnisse getrennt voneinander in die Gleichung einsetzen und ausrechnen.
Quellen und Hilfen im Internet
Herr Beckers, unser Mathelehrer ;)
www.ardnt-bruenner.de/mathe/9/quadratischegleichungen.html
www.Mathepower.com/qgleich.php
www.lehrer-online.de/quadratische-funktionen-gleichungen.php
von Rachel Liven und Lukas F.

