Spatprodukt: Unterschied zwischen den Versionen

Version vom 1. Dezember 2009, 12:26 Uhr

Volumen eines Spats

Mit dem Spatprodukt kann man das Volumen eines Spates, der von drei linear unabhängigen Vektoren aufgespannt wird, berechnen.

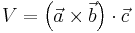
$V = \left(\vec{a}\times\vec{b}\right)\cdot\vec{c}$

Zur Berechnung des Kreuzproduktes 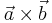$\vec{a}\times\vec{b}$ und des Skalarproduktes 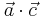$\vec{a}\cdot\vec{c}$ siehe hier.

Ein Beispiel:

Volumen von Pyramiden

Mit dem Spatprodukt kann man außerdem auch das Volumen einer Pyramide berechnen:

Dreiseitige Pyramide:

$V = \frac{1}{6}\cdot\left[\left(\vec{a}\times\vec{b}\right)\cdot\vec{c}\right]$

Vierseitige Pyramide:

$V = \frac{1}{3}\cdot\left[\left(\vec{a}\times\vec{b}\right)\cdot\vec{c}\right]$

Version vom 1. Dezember 2009, 12:25 Uhr (Quelltext anzeigen) Lea K. (Diskussion \| Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 1. Dezember 2009, 12:26 Uhr (Quelltext anzeigen) Lea K. (Diskussion \| Beiträge) Zum nächsten Versionsunterschied →
Zeile 6:		Zeile 6:

	Zur Berechnung des Kreuzproduktes <math>\vec{a}\times\vec{b}</math> und des Skalarproduktes <math>\vec{a}\cdot\vec{c}</math> siehe [http://wikis.zum.de/kas/index.php/Skalarprodukt%2C_Vektorprodukt hier].		Zur Berechnung des Kreuzproduktes <math>\vec{a}\times\vec{b}</math> und des Skalarproduktes <math>\vec{a}\cdot\vec{c}</math> siehe [http://wikis.zum.de/kas/index.php/Skalarprodukt%2C_Vektorprodukt hier].
		+
		+	''Ein Beispiel:''
		+