Die Nr 1: Unterschied zwischen den Versionen
(→Ergebnis aus Station Nummer 4) |
(→Ergebnis aus Station Nummer 4) |
||
| Zeile 22: | Zeile 22: | ||
Diese Station war von relativ großer Bedeutung da man die Durschnittsgeschwindigkeit dazu benutzen kann, besser bestimmen zu können wie weit das Auto vorraussichtlich fährt. | Diese Station war von relativ großer Bedeutung da man die Durschnittsgeschwindigkeit dazu benutzen kann, besser bestimmen zu können wie weit das Auto vorraussichtlich fährt. | ||
| + | |||
| + | |||
| + | |||
| + | === Ergebnis aus Station Nummer 5 === | ||
| + | Hierbei ging es um Energie und Kraft. Zwei wichtige Formeln gab es bei dieser Station: | ||
| + | <math>\Delta</math>''E'' = ''F'' * <math>\Delta</math>''s'' | ||
| + | <math>\rightarrow</math> Übertragene Energie = Kraft mal zurückgelegte Strecke | ||
| + | |||
| + | Es gilt: | ||
| + | 1 J = 1 N * m | ||
| + | |||
| + | Mithilfe einer speziellen Rechnung berechneten wir wieviel Kraft wir in die Mausefalle gesteckt haben: | ||
| + | <math>\Delta</math>''E'' = 2 N * 0.01m + 3 N * 0.01m + ... + 14 N * 0.01m = 1.04 J | ||
Version vom 6. Juni 2012, 09:47 Uhr
Inhaltsverzeichnis |
Mausefallenauto - von den Experimenten zu den Ergebnissen
Ergebnis aus Station Nummer 1
Bei dem ersten Experiment haben wir getestet, wieviel Kraft (F, in Newton) benötigt wird, um einen Holzklotz (ca. 145g schwer) über verschiedene Oberflächen gleichmäßig zu ziehen. Zum Messen haben wir Kraftmesser verwendet. Beim zweiten Experiment wollten wir wissen, wieviel Kraft man bei bestimmten Gewichten benötigt, indem wir nach und nach Gewichte drauf gestapelt haben. Als letztes fanden wir die Haftreibung, die Rollreibung und die Gleitreibung des Holzklotzes heraus.
Die wichtigen Ergebnisse dieser Station waren für uns die Reibung der Oberfläche auf der wir das Auto später fahren lassen, und so konnten wir außerdem überlegen welches Material wir für das Mausefallenauto, beziehungsweise Reifen nehmen wollen, und welches Gewicht das Auto vorzugsweise haben sollte.
Ergebnis aus Station Nummer 3
Bei Experiment 1 fanden wir heraus, welche Reibungskraft ('FReibung) auftritt wenn wir das Mausefallenauto gleichmäßig über den Tisch/Boden ziehen. Unser Ergebnis war: 0.02N (Newton). Das bedeutete für uns das wir mit Experiment 2 beginnen konnten. Unser Schluss aus Experiment 2 war dass wir das Auto in einem "großen Gang" fahren lassen sollten, was zwar bedeutet, dass mehr Energie benötigt wird, dafür aber sich die Schubkraft erhöht, weil man dann mehr Kraft rein steckt. Aus Experiment 3 haben wir geschlossen dass wir einen möglichst langen Hebel brauchen, und das Auto kurz gehalten werden sollte, aber auch nicht zu kurz, sondern auf die Länge des Hebels abgestimmt. In Experiment 4 haben wir herausgefunden, wie man eine optimale Hebellänge finden kann. Dazu rechnet man den Radius des Rads (rR) mal die FReibung die 0.1N. Das Ergebnis war dass unser Hebel mit einer Kraft von 0.22 an der Achse ziehen muss, die genaue Hebellänge muss man jetzt durch ausprobieren herausfinden.
Ergebnis aus Station Nummer 4
Sinn der Station 4 war die Durchschnittsgeschwindigkeit unseres Mausefallenautos herauszufinden. Das geht mit der Formel Durchschnittsgeschwindigkeit = Strecke / Geschwindigkeit. Um das zu messen, lässt man das Mausefallenauto am besten mehrere Male fahren und misst dabei sowohl die Geschwindigkeit als auch wie weit es fährt. Aus diesen Ergebnissen errechnet man den Durschnitt, um dann die endgültige Rechnung durchführen zu können.
Diese Station war von relativ großer Bedeutung da man die Durschnittsgeschwindigkeit dazu benutzen kann, besser bestimmen zu können wie weit das Auto vorraussichtlich fährt.
Ergebnis aus Station Nummer 5
Hierbei ging es um Energie und Kraft. Zwei wichtige Formeln gab es bei dieser Station:
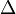E = F * 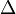s
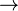Übertragene Energie = Kraft mal zurückgelegte Strecke
Es gilt: 1 J = 1 N * m
Mithilfe einer speziellen Rechnung berechneten wir wieviel Kraft wir in die Mausefalle gesteckt haben:
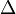E = 2 N * 0.01m + 3 N * 0.01m + ... + 14 N * 0.01m = 1.04 J
