Intergrationsmethoden: Unterschied zwischen den Versionen
Aus KAS-Wiki
Eda A. (Diskussion | Beiträge) |
Eda A. (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
1. Partielle Integration: | 1. Partielle Integration: | ||
| + | <math> | ||
| + | \int_{a}^b \mathrm u(x)* v'(x)\,\mathrm dx =[u(x)* v(x)]_a^b- \int_{a}^b \mathrm u'(x)*v(x)\,\mathrm dx | ||
| + | </math> | ||
| − | + | Beispiel: | |
| − | + | <math> | |
| + | \int_{-1}^4 \mathrm (2x+1)* e^x\,\mathrm dx </math> | ||
| + | = <math>[(2x+1)*e^x]_{-1}^4- \int_{-1}^4 \mathrm 2*e^x\,\mathrm dx</math> | ||
| + | = <math>[(2x+1)*e^x-2*e^x]_{-1}^4</math> | ||
| + | = <math>[382,184]-[-1,1037] | ||
| + | = 383,29 F.E.</math> | ||
| − | + | ||
| − | + | 2. Substitution: | |
| − | + | ||
| − | + | Beispiel: | |
| − | + | ||
Version vom 3. Dezember 2009, 10:53 Uhr
1. Partielle Integration:
![\int_{a}^b \mathrm u(x)* v'(x)\,\mathrm dx =[u(x)* v(x)]_a^b- \int_{a}^b \mathrm u'(x)*v(x)\,\mathrm dx](/images/math/4/c/a/4ca2d7d9f35a1bab5533c273734a279d.png)
Beispiel:
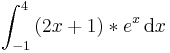 =
= ![[(2x+1)*e^x]_{-1}^4- \int_{-1}^4 \mathrm 2*e^x\,\mathrm dx](/images/math/4/6/4/4641126b33e9264e6d665a5945540fad.png) =
= ![[(2x+1)*e^x-2*e^x]_{-1}^4](/images/math/8/3/8/8384b7d728f13a53ce4fd0113e5a5dd8.png) =
= ![[382,184]-[-1,1037]
= 383,29 F.E.](/images/math/a/d/0/ad05044bc3445a8c9d0ead24288fce64.png)
2. Substitution:
Beispiel:

