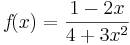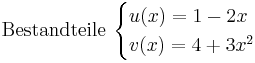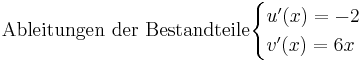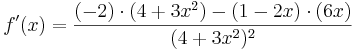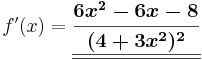Ableitungsregeln: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
Zeile 18: Zeile 18:
 
=== Faktorregel ===
 
=== Faktorregel ===
  
−
<math>f\!(x)=k*g(x)</math>
+
<math>f\!(x)=k \cdot g(x)</math>
  
−
=> <math>f\!\,'(x)=k*g'(x)</math>
+
=> <math>f\!\,'(x)=k \cdot g'(x)</math>
  
  
Zeile 33: Zeile 33:
 
=== Produktregel ===
 
=== Produktregel ===
  
−
<math>f\!(x)=u(x)*v(x)</math>
+
<math>f\!(x)=u(x) \cdot v(x)</math>
  
−
=> <math>f\!\,'(x)=u'(x)*v(x)+u(x)*v'(x)</math>
+
=> <math>f\!\,'(x)=u'(x) \cdot v(x)+u(x) \cdot v'(x)</math>
  
  
Zeile 43: Zeile 43:
  
  
−
=> <math>f\!\,'(x)=\frac{u'(x)*v(x)-u(x)*v'(x)}{(v(x))^2}</math>
+
=> <math>f\!\,'(x)=\frac{u'(x) \cdot v(x)-u(x) \cdot v'(x)}{(v(x))^2}</math>
  
  
Zeile 50: Zeile 50:
 
<math>f\!(x)=g(h(x))</math>
 
<math>f\!(x)=g(h(x))</math>
  
−
=> <math>f\!\,'(x)=h'(x)*g'(h(x))</math>
+
=> <math>f\!\,'(x)=h'(x) \cdot g'(h(x))</math>
  
  
Zeile 57: Zeile 57:
 
<math>f\!^-\,^1(y)\ \mathrm{sei\ die\ Umkerhfunktion\ zu\ y=f(x)}</math>
 
<math>f\!^-\,^1(y)\ \mathrm{sei\ die\ Umkerhfunktion\ zu\ y=f(x)}</math>
  
−
<math>(\!f\!^-\,^1)'(f(x))=\frac{1}{f'(x)}\ \mathrm{oder}\ (\!f\!^-\,^1)'(f\!(x))*f\!\,'(x)=1</math>
+
<math>(\!f\!^-\,^1)'(f(x))=\frac{1}{f'(x)}\ \mathrm{oder}\ (\!f\!^-\,^1)'(f\!(x)) \cdot f\!\,'(x)=1</math>
  
  
Zeile 76: Zeile 76:
  
  
−
<math>f\!(x)=(4x^3-2x+1)*(x^2-2x+5)</math>
+
<math>f\!(x)=(4x^3-2x+1) \cdot (x^2-2x+5)</math>
  
  
Zeile 91: Zeile 91:
  
  
−
<math>f\!\,'(x)=(12x^2-2)*(x^2-2x+5)+(4x^3-2x+1)*(2x-2)</math>
+
<math>f\!\,'(x)=(12x^2-2) \cdot (x^2-2x+5)+(4x^3-2x+1) \cdot (2x-2)</math>
  
 
<math>f\!\,'(x)=12x^4-24x^3+60x^2-2x^2+4x-10+8x^4-8x^3-4x^2+4x+2x-2</math>
 
<math>f\!\,'(x)=12x^4-24x^3+60x^2-2x^2+4x-10+8x^4-8x^3-4x^2+4x+2x-2</math>
Zeile 102: Zeile 102:
  
  
−
<math>f\!(x)=\sin(x)*\cos(x)</math>
+
<math>f\!(x)=\sin(x) \cdot \cos(x)</math>
  
 
<math>\mathrm{Bestandteile}\ \begin{cases}
 
<math>\mathrm{Bestandteile}\ \begin{cases}
Zeile 116: Zeile 116:
  
  
−
<math>f\!\,'(x)=\cos(x)*\cos(x)+\sin(x)*(-\sin(x))</math>
+
<math>f\!\,'(x)=\cos(x) \cdot \cos(x)+\sin(x) \cdot (-\sin(x))</math>
  
 
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{\cos^2(x)-\sin^2(x)}}}</math>
 
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{\cos^2(x)-\sin^2(x)}}}</math>
Zeile 124: Zeile 124:
  
  
−
<math>f\!(x)=x^n*e^{x}</math>
+
<math>f\!(x)=x^n \cdot e^{x}</math>
  
 
<math>\mathrm{Bestandteile}\ \begin{cases}
 
<math>\mathrm{Bestandteile}\ \begin{cases}
Zeile 133: Zeile 133:
  
 
<math>\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases}
 
<math>\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases}
−
u'(x)=n*x^{n-1}\\
+
u'(x)=n \cdot x^{n-1}\\
 
v'(x)=e^{x}
 
v'(x)=e^{x}
 
\end{cases}</math>
 
\end{cases}</math>
  
  
−
<math>f\!\,'(x)=(n*x^{n-1})*(e^{x})+(x^n)*(e^{x})</math>
+
<math>f\!\,'(x)=(n \cdot x^{n-1}) \cdot (e^{x})+(x^n) \cdot (e^{x})</math>
  
−
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1}*e^{x}*(n+x)}}}</math>
+
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1} \cdot e^{x} \cdot (n+x)}}}</math>
  
  
Zeile 168: Zeile 168:
  
  
−
<math>f\!\,'(x)=\frac{(-2)*(4+3x^2)-(1-2x)*(6x)}{(4+3x^2)^2}</math>
+
<math>f\!\,'(x)=\frac{(-2) \cdot (4+3x^2)-(1-2x) \cdot (6x)}{(4+3x^2)^2}</math>
  
 
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{\frac{6x^2-6x-8}{(4+3x^2)^2}}}}</math>
 
<math>f\!\,'(x)=\boldsymbol{\underline{\underline{\frac{6x^2-6x-8}{(4+3x^2)^2}}}}</math>

Version vom 3. Dezember 2009, 11:02 Uhr

Inhaltsverzeichnis

Ableitungsregeln

Potenzregel

f\!(x)=x^n

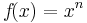
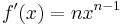
=> f\!\,'(x)=nx^{n-1}


Summenregel

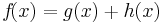
f\!(x)=g(x)+h(x)

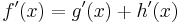
=> f\!\,'(x)=g'(x)+h'(x)


Faktorregel

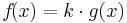
f\!(x)=k \cdot g(x)

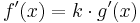
=> f\!\,'(x)=k \cdot g'(x)


Differenzregel

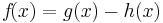
f\!(x)=g(x)-h(x)

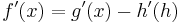
=> f\!\,'(x)=g'(x)-h'(h)


Produktregel

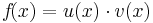
f\!(x)=u(x) \cdot v(x)

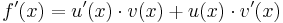
=> f\!\,'(x)=u'(x) \cdot v(x)+u(x) \cdot v'(x)


Quotientenregel

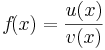
f\!(x)=\frac{u(x)}{v(x)}


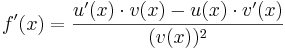
=> f\!\,'(x)=\frac{u'(x) \cdot v(x)-u(x) \cdot v'(x)}{(v(x))^2}


Kettenregel

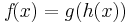
f\!(x)=g(h(x))

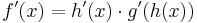
=> f\!\,'(x)=h'(x) \cdot g'(h(x))


Umkehrregel

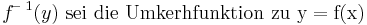
f\!^-\,^1(y)\ \mathrm{sei\ die\ Umkerhfunktion\ zu\ y=f(x)}

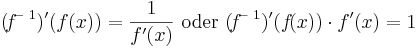
(\!f\!^-\,^1)'(f(x))=\frac{1}{f'(x)}\ \mathrm{oder}\ (\!f\!^-\,^1)'(f\!(x)) \cdot f\!\,'(x)=1


Beispiele

Summenregel

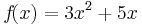
f\!(x)=3x^2+5x

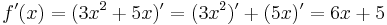
=> f\!\,'(x)=(3x^2+5x)'=(3x^2)'+(5x)'=6x+5


Produktregel

Beispiel 1

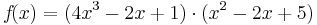
f\!(x)=(4x^3-2x+1) \cdot (x^2-2x+5)


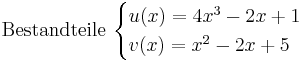
\mathrm{Bestandteile}\ \begin{cases} u(x)=4x^3-2x+1\\ v(x)=x^2-2x+5 \end{cases}


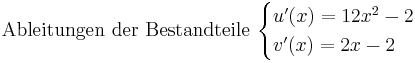
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=12x^2-2\\ v'(x)=2x-2 \end{cases}


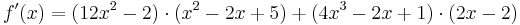
f\!\,'(x)=(12x^2-2) \cdot (x^2-2x+5)+(4x^3-2x+1) \cdot (2x-2)

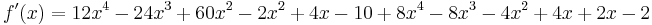
f\!\,'(x)=12x^4-24x^3+60x^2-2x^2+4x-10+8x^4-8x^3-4x^2+4x+2x-2

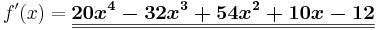
f\!\,'(x)=\boldsymbol{\underline{\underline{20x^4-32x^3+54x^2+10x-12}}}


Beispiel 2

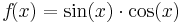
f\!(x)=\sin(x) \cdot \cos(x)

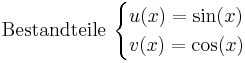
\mathrm{Bestandteile}\ \begin{cases} u(x)=\sin(x)\\ v(x)=\cos(x) \end{cases}


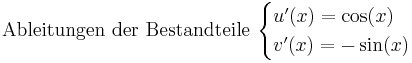
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=\cos(x)\\ v'(x)=-\sin(x) \end{cases}


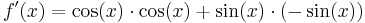
f\!\,'(x)=\cos(x) \cdot \cos(x)+\sin(x) \cdot (-\sin(x))

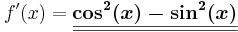
f\!\,'(x)=\boldsymbol{\underline{\underline{\cos^2(x)-\sin^2(x)}}}


Beispiel 3

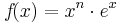
f\!(x)=x^n \cdot e^{x}

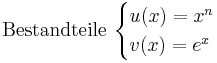
\mathrm{Bestandteile}\ \begin{cases} u(x)=x^n\\ v(x)=e^{x} \end{cases}


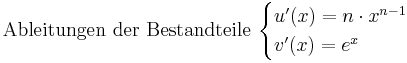
\mathrm{Ableitungen\ der\ Bestandteile}\ \begin{cases} u'(x)=n \cdot x^{n-1}\\ v'(x)=e^{x} \end{cases}


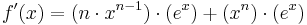
f\!\,'(x)=(n \cdot x^{n-1}) \cdot (e^{x})+(x^n) \cdot (e^{x})

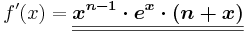
f\!\,'(x)=\boldsymbol{\underline{\underline{x^{n-1} \cdot e^{x} \cdot (n+x)}}}


Quotientenregel

Beispiel

f\!(x)=\frac{1-2x}{4+3x^2}

\mathrm{Bestandteile}\ \begin{cases} u(x)=1-2x\\ v(x)=4+3x^2 \end{cases}


\mathrm{Ableitungen\ der\ Bestandteile} \begin{cases} u'(x)=-2\\ v'(x)=6x \end{cases}


f\!\,'(x)=\frac{(-2) \cdot (4+3x^2)-(1-2x) \cdot (6x)}{(4+3x^2)^2}

f\!\,'(x)=\boldsymbol{\underline{\underline{\frac{6x^2-6x-8}{(4+3x^2)^2}}}}

Von „http://kas.zum.de/index.php?title=Ableitungsregeln&oldid=351“