Der Artikel der 9b: Unterschied zwischen den Versionen
Aila.F (Diskussion | Beiträge) (→Elektrische Größen) |
(→Wir untersuchen: Was ist Strom?) |
||
| Zeile 12: | Zeile 12: | ||
2. Elektroskop<br />Wir reiben ein Lineal an einem Tuch um es statisch aufzuladen. Danach halten wir es einige Millimeter über das Elektroskop(1)*. Der Zeiger im Elektroskop bewegt sich, wenn man dann eine Hand auf das oben angebrachte Metallplättchen legt, steht es wieder still. Dies passiert, da nun ein Kontakt zur Erde besteht und sich das Elektroskop entladen kann. Das Stäbchen kehrt in seine Ausgangsposition zurück. | 2. Elektroskop<br />Wir reiben ein Lineal an einem Tuch um es statisch aufzuladen. Danach halten wir es einige Millimeter über das Elektroskop(1)*. Der Zeiger im Elektroskop bewegt sich, wenn man dann eine Hand auf das oben angebrachte Metallplättchen legt, steht es wieder still. Dies passiert, da nun ein Kontakt zur Erde besteht und sich das Elektroskop entladen kann. Das Stäbchen kehrt in seine Ausgangsposition zurück. | ||
| + | |||
| + | |||
| + | [[Datei:Elektroskop.jpg|thumb|Elektroskopexperiment]] | ||
| + | |||
| + | |||
| + | [[Datei:Elektroskop2.jpg|thumb|Elektroskopexperiment mit Lineal]] | ||
| + | |||
| + | |||
| + | [[Datei:Elektroskop3.jpg|thumb|Elektroskop mit Finger]] | ||
| + | |||
Welche Wirkungen hat Strom? Auf den menschlichen Körper kann Strom viele unterschiedliche Wirkungen haben. Einerseits ist Strom extrem gefährlich für uns. Schon kleine Ströme von "nur" 20-30 Volt können sehr gefährlich sein, doch Strom kann auch Leben retten. Durch Stromstösse können Herzrythmusstörungen beendet werden. Jedoch hat Strom noch weitere andere Wirkungen.<br /> | Welche Wirkungen hat Strom? Auf den menschlichen Körper kann Strom viele unterschiedliche Wirkungen haben. Einerseits ist Strom extrem gefährlich für uns. Schon kleine Ströme von "nur" 20-30 Volt können sehr gefährlich sein, doch Strom kann auch Leben retten. Durch Stromstösse können Herzrythmusstörungen beendet werden. Jedoch hat Strom noch weitere andere Wirkungen.<br /> | ||
| + | |||
1. Die Wärmewirkung<br /> | 1. Die Wärmewirkung<br /> | ||
Wenn man eine Lampe mit Strom durch fliessen lässt, merkt man nach kurzer Zeit deutliche Wärme an der Glühbirne. | Wenn man eine Lampe mit Strom durch fliessen lässt, merkt man nach kurzer Zeit deutliche Wärme an der Glühbirne. | ||
Version vom 20. Mai 2015, 11:38 Uhr
Inhaltsverzeichnis |
Wir untersuchen: Was ist Strom?
Wir haben mit zwei verschiedenen Experimenten untersucht, wie man Strom erkennen kann und was Strom für uns ist.
1. Luftballonexperiment
Wir reiben zwei Luftballons mit einem Tuch ein und binden beide an eine Schnur (die beide Luftballons verbindet). Wir haben versucht die Luftballons gegeneinander zu schwingen, doch die beiden Luftballons stoßen sich ab, das heisst, dass die Luftballons die gleiche Ladung haben. Berührt man mit dem geladenen Luftballon eine neutrale Fläche fließen bei einer negativen Ladung die Elektronen vom Ballon auf die neutrale Fläche. Bei einer positiven Ladung zieht der Ballon aus der Fläche so viele Elektronen wie er benötigt um wieder neutral zu werden. Nun werden sich die Ballons nicht mehr abstoßen.
2. Elektroskop
Wir reiben ein Lineal an einem Tuch um es statisch aufzuladen. Danach halten wir es einige Millimeter über das Elektroskop(1)*. Der Zeiger im Elektroskop bewegt sich, wenn man dann eine Hand auf das oben angebrachte Metallplättchen legt, steht es wieder still. Dies passiert, da nun ein Kontakt zur Erde besteht und sich das Elektroskop entladen kann. Das Stäbchen kehrt in seine Ausgangsposition zurück.
Welche Wirkungen hat Strom? Auf den menschlichen Körper kann Strom viele unterschiedliche Wirkungen haben. Einerseits ist Strom extrem gefährlich für uns. Schon kleine Ströme von "nur" 20-30 Volt können sehr gefährlich sein, doch Strom kann auch Leben retten. Durch Stromstösse können Herzrythmusstörungen beendet werden. Jedoch hat Strom noch weitere andere Wirkungen.
1. Die Wärmewirkung
Wenn man eine Lampe mit Strom durch fliessen lässt, merkt man nach kurzer Zeit deutliche Wärme an der Glühbirne.
2. Die Leuchtwirkung
Wird eine Lampe mit Strom versorgt, fängt sie an zu leuchten.
3. Die magnetische Wirkung des elektrischen Stroms
Kurzes Experiment: Hält man einen Magneten an eine eingeschaltetete Glühbirne, schwingt der Glühwedel hin und her. Bei der ausgeschaltenen Glühbirne ist dies nicht der Fall, daraus schliessen wir, dass der Strom eine magnetische Wirkung haben muss.
Für uns ist elektrischer Strom, Ladungen die durch Kabel fließen.
(1) Elektroskop :
Zum Nachweis der Menge an elektrischer Ladung dient ein Elektroskop. In einem offenen Gehäuse befindet sich eine vertikale Metallstange, an der ein beweglicher Zeiger befestigt ist. Dieser ist unten etwas schwerer, so dass er senkrecht stehen bleibt. Bringt man die obere Platte mit einem negativ geladenen Körper in Verbindung (z.B. Ein Lineal), so verteilen sich die abfließenden Elektronen sowohl auf dem Stab, als auch auf den Zeiger. Der Zeiger bewegt sich.
Elektrische Größen
In dem letzten Wikiartikel wurde die Frage "Was ist Strom?" behandelt. Wir beschäftigen uns nun mit den Fragen "Was sind elektrische Größen?" und "Wie kann man zur Veranschaulichung einen elektrischen Stromkreis mit einen Wasserkreislauf vergleichen?"
Bei dem Luftballonexperiment ging von einem Tuch eine Ladung auf den Luftballon über. Auch als dann der Luftballon die Hand berührte wurde die Ladung, welche nun auf dem Luftballon war, auf die Hand übertragen. Elektrische Ladung kann also abgegeben werden, sich "fortbewegen" Die Anzahl an Elektronen, die, in einer bestimmten Zeit, an einer bestimmten Stelle vorbeifließen, bezeichnen wir als elektrische Spannung. Genauso lässt sich auch erklären warum sich der Zeiger des Elektroskops bewegt. Die Ladung wird übertragen.
Die elektrische Spannung (U) wird in (V) gemessen und gibt an wie viel Energie eine einzige Ladung trägt (U V=J:C).
Die elektrische Stromstärke (I) wird in (A) gemessen und gibt an wieviele Elektronen, also Ladungen, insgesamt an einer bestimmten Stelle, in einer gewissen Zeit, vorbeifließt. (I A=C:S)
Die elektrische Leistung (P) wird in (W) gemessen und gibt an wieviel Energie insgesamt an einem bestimmten Ort pro Zeit vorbeifließt. Hierzu multipliziert man U und I (P W=J:S)
Der Widerstand beschreibt die Leitfähigkeit (R Ohm=V:A)'''
Vereinfacht kann man sagen, dass physikalische Größen in verschiedenen Einheiten gemessen werden und sie verschiedene Formelzeichen haben.
Als erstes muss man verstehen was Strom überhaupt ist, damit man verstehen kann wie wir uns die Tabelle (siehe unten) hergeleitet haben. Jeder kennt das Beispiel das eine Lampe leuchtet wenn sie an einen Stromkreis angeschlossen ist und Strom fließt. Durch einen Kreislauf fließt Energie, welche von elektrischen Ladungen transportiert wird.
Die elektrische Spannung gibt an wieviel Energie eine einzige Ladung trägt.
Wenn man eine Lampe zum leuchten bringen möchte, braucht man eine Quelle welche Strom abgibt. Die elektrische Leistung wird errechnet indem der elektrische Strom mit der elektrischen Spannung mulitpliziert wird.
Der elektrische Strom gibt an wie viele Elektronen, Ladungen, durch ein Kabel fließt. Vereinfacht kann man sagen je mehr Elektronen durch ein Kabel fließen, desto größer ist die elektrische Spannung.
Der Wiederstand gibt an wie gut ein Kabel leitet. Die Leitfähigkeit ist von Faktoren, wie dem Material und dem Querschnitt, abhängig.
| Formelzeichen | physikalische Größen | Einheit |
|---|---|---|
| U | elektrische Spannung | V=J:C |
| P | elektrische Leistung | W=J:S |
| I | elektrische Stromstärke | A=C:S |
| R | elektrischer Widerstand | O=V:A |
V=Volt
W=Watt
A=Ampere
J=Energie
S=Sekunde
C=Coulomb
O=Ohm
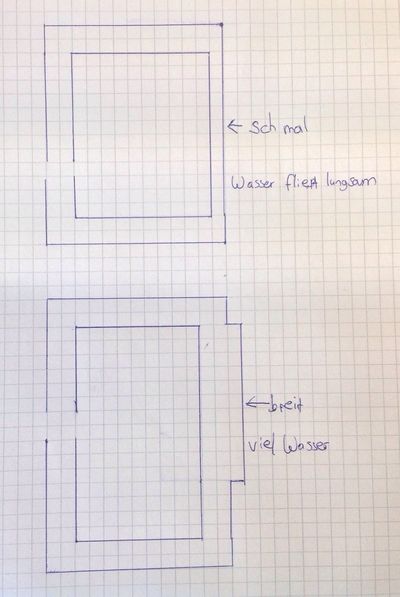
Wie kann man einen elektrischen Stromkreis mit einem Wasserkreislauf vergleichen?
Einen Stromkreislauf kann man zur Veranschaulichung mit einem Wasserkreislauf vergleichen.
Die elektrische Spannung kann man auf einen Wasserkreislauf beziehen, weil auch in einem Wasserkreislauf die Spannung genau die gleiche Rolle spielt wie in einem elektrischen Kreislauf. Die Stromstärke gibt nämlich an wie viel Energie ein einzelnes Wasserteilchen hat. Die Spannung ist der Wasserdruck in der Leitung.
Die elektrische Leistung kann man auf einen Wasserkreislauf beziehen, weil man dort sehen kann wie viel Wasser pro Zeit aus einer Wasserquelle heraus fließt.
Dieelektrische Stromstärke kann auf einen Wasserkreislauf bezogen werden, da sie die durchfließende Wassermenge pro Zeit an einer bestimmten Stelle des Wasserkreislaufesangibt,also je mehr Wasser destso grösser ist die Stromstärke.Dies ist in einem Stromkreis das selbe Prinzip.
Den elektrischen Wiederstand kann man im Wasserkreislauf mit einem Rohr vergleichen. Faktoren die den regelmäßigen Fluss beeinflussen sind Querschnitt und Material.
Die nächste Gruppe wird sich auf Dräthe und deren Leitfähigkeit beziehen.
Die elektrischen Größen in Reihen- und Parallelschaltung
Wir haben uns mit dem Thema Strom und Leitfähigkeit beschäftigt. Es gibt zwei verschiedene Schaltungen: Die Reihen- und die Parallelschaltung.
Bei einer Reihenschaltung mit drei Lampen ist die Leistung geringer als bei einer Reihenschaltung mit zwei Lampen, während bei einer Parallelschaltung mit zwei Lampen die Leistung geringer ist, als bei drei Lampen.
Reihenschaltung Die elektrische Stromstärke und die elektrische Spannung bleiben bei den einzelnen Lampen gleich. Wenn man die Stromstärke aller Lampen addiert, erhält man als Summe die Stromstärke der Quelle.
Parallelschaltung Bei der Parallelschaltung ist die Stromstärke pro Lampe identisch. Die Leistung, genauso wie die Spannung, bleibt ebenfalls gleich (Quelle und Lampe). Je mehr Lampen sich im Stromkreis befinden, desto höher wird die Stromstärke. Nun, da ihr die beiden Schaltungen kennt werden wir euch hier ein Experiment zeigen: Wir haben eine Reihen- und Parallelschaltung mit zwei Lampen aufgebaut. Dabei kam heraus, dass zwei Lampen weniger elektrische Leistung haben, als drei Lampen in den Schaltungen.
Experiment zum Energietransport: Im Experiment zum Energietransport haben wir ein Steckfeld mit überträgern und Lampen gefüllt. Dazu haben wir zwischen die Lampen ein Multimeter geschaltet, daraufhin haben wir gemessen wie viel Strom herein kommt und wieder hinaus fließt. Darüber hinaus geben wir an wie viel Strom noch aus der Quelle kommt. Dies haben wir mit der Parallel und der Reihenschaltung ausprobiert. Wir sind zu diesen Ergebnissen gelangt: Reihenschaltung A V W 1 Lampe 0,17 5 0,85 2 Lampe 0,17 5 0,85 3 Lampe 0,17 5 0,85 4 Lampe 0,17 5 0,85 Quelle 0,72 5 3,29
Reihenschaltung A V W 1 Lampe 0,17 5 0,85 2 Lampe 0,17 5 0,85 3 Lampe 0,17 5 0,85 4 Lampe 0,17 5 0,85 Quelle 0,72 5 3
Parallelschaltung A V W 1 Lampe 0,21 7,17 1,5 2 Lampe 0,21 7,15 1,5 3 Lampe 0,21 7.15 1,5 4 Lampe 0,21 7,15 1,5 Quelle 0,8 7,15 5,
Parallelschaltung A V W 1 Lampe 0,21 7,17 1,5 2 Lampe 0,21 7,15 1,5 3 Lampe 0,21 7.15 1,5 4 Lampe 0,21 7,15 1,5 Quelle 0,8 7,15 5,8 Um dies nun alles auszurechnen haben wir eine neue Formel gefunden Wir haben die Formel f(x)= m*x Wenn wir jetz für x in unserm Fall 5 einsetzen und für m 0,02 einsetzen bildet sich die Formel F(x)= 0,02*5 Wenn man die Stromstärke mit der Spanung multipliziert,ergibt sich die elektrische Leistung:I x U= P Eine Reihenschaltung braucht mehr elektrische Leistung als eine Parallelschaltung
Ohmsches Gesetz
Durch den vorherigen Versuch, kamen wir zu diesen Überlegungen.
Ein proportionaler Zusammenhang bedeutet, dass wenn sich eine Größe durch einen Faktor verändert, verändert sich auch die andere Größe um denselben Faktor. Das bedeutet also, dass auch ein Zusammenhang zwischen U und I besteht. (Wenn sich dann also I ändert, dann auch U ).
Erster Schritt: Wir haben einen Stromkreis aufgebaut (nur mit einer Lampe). Dann haben wir die Stromstärke (an der Quelle) und die elektrische Leistung (im Stromkreis) gemessen.
I = elektrische Stromstärke
U = elektrische Spannung
Schließlich haben wir versucht einen funktionalen Zusammenhang zwischen Widerstand, elektrischer Stromstärke und Spannung herauszufinden , anhand einer WERTETABELLE und einer ZEICHNUNG VON EINEM GRAPHEN.
| Quelle | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|
| Lampe (Standard) | 0,04 | 0,06 | 0,07 | 0,08 | 0,09 | 0,1 | 0,12 | 0,13 | 0,14 | 0,15 |
| Widerstand (47) | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,1 | 0,11 |
| Widerstand (100) | 0,01 | 0,02 | 0,02 | 0,03 | 0,03 | 0,04 | 0,04 | 0,05 | 0,05 | 0,06 |
Wir haben für die Ergebnisse mehrere Lampen benutzt: ,,Normale Lampe", ,,47er Widerstand", ,,100er Widerstand"
Dadurch haben wir verschiedene Ergebnisse herausgefunden. (Siehe Links unten)
Wir kamen zum Entschluss, dass alle Graphen durch den 0-Punkt gehen, deshalb ist es eine Proportionale Funktion.
Allgemeine Formel für die Proportionale Funktion: 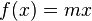
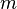 steht hier für die Steigung innerhalb der einzelnen Punkte
steht hier für die Steigung innerhalb der einzelnen Punkte
Das 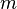 findet man heraus indem man die Formel:
findet man heraus indem man die Formel:
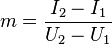
benutzt.
Setzt man nun für 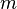 = 0.02 ein, entsteht die Formel:
= 0.02 ein, entsteht die Formel:
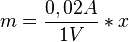 <-gilt für die 47-Lampe
<-gilt für die 47-Lampe
Kehrwert: 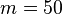
Da der Kehrwert 50 beträgt, besteht ein Zusammenhang zwischen dem Widerstand und der gemessenen Größe ( 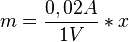 )
)
So kann man den Graphen weiterführen (man kann weitere Zahlen einsetzen und dies anhand einer Rechnung herausfinden)
Wenn man den Kehrwert anwendet kommt man zur Formel des Ohm-Zeichen.
Die größe hier heißt ,,elektrischer Widerstand
Formelzeichen = 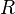 Ω
Ω 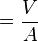
Ω = Ohm-Zeichen
Zusammenhang zwischen U,I,R: 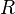
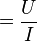
Dies ist das Ohmsche Gesetz
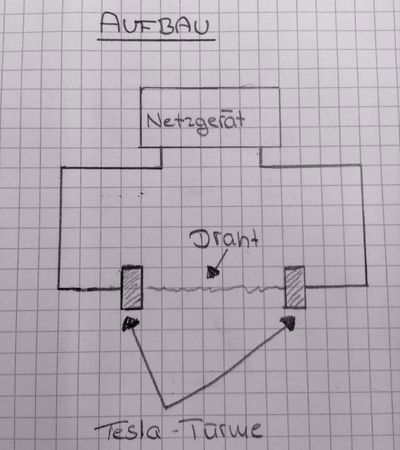
Das Draht Experiment
Jetzt haben wir versucht eine Regelmäßigkeit zwischen den physikalischen Größen U, I und R zu finden, indem wir einen Stromkreis aufgebaut haben, in welchen wir zwei Tesla-Türme eingebaut und zwischen sie nacheinander drei verschieden lange Drähte eingespannt haben (25cm, 50cm, 100cm). Beim längsten Draht war die elektrische Stromstärke am geringsten, beim Kürzesten am höchsten. Das heißt, dass längere Drähte mehr elektrische Stromstärke brauchen um die gleiche Spannung zu erreichen wie kürzere Drähte. Ein weiterer Grund ist, dass der Draht viel dünner ist, als der Rest der Kabel im Stromkreis. Der Strom wird also von einem normalen Draht in ein viel dünneren Draht geleitet und braucht mehr Stromstärke um durch die Verengung zukommen.
Aus den zwei Werten haben wir dann R also den Widerstand berechnet.
| Länge | U | I | R |
|---|---|---|---|
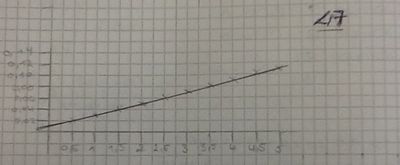
| 25cm | 2 | 1,23 | 1,63 |
| 3,8 | 2,34 | 1,63 | |
| 5,8 | 3,61 | 1,61 | |
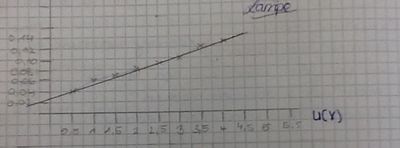
| 50cm | 2 | 0,69 | 2,9 |
| 3,8 | 1,29 | 2,95 | |
| 5,8 | 1,99 | 2,91 | |
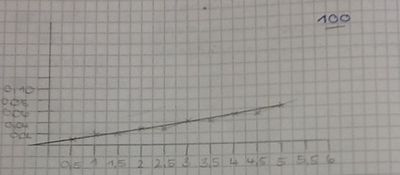
| 100cm | 2 | 0,33 | 6,1 |
| 3,8 | 0,62 | 6,13 | |
| 5,8 | 0,99 | 5,9 |
Die Werte sind ausschließlich Messwerte und daher nicht zu 100% genau!
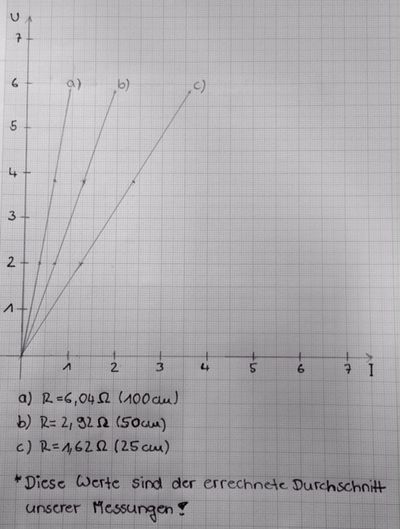
Wir haben für jeden Graphen einen Funktionsterm gefunden:
a) 100cm: f(x)=6,125x
b) 50cm: f(x)=3x
c) 25cm: f(x)=1,625x
U= elektrische Spannung P= elektrische Leistung I=elektrische Stromstärke V=Volt O=Ohm
Funktionale Zusammenhänge + physikalische Größen aus einem Experiment ableiten
Wenn zwei Größen funktional zusammenhängend sind, dann verändern sich die Größen immer verhältnismäßig gleich zueinander. Beispiel A: Addiert man zu Größe 1 den Wert 2, addiert sich zur Größe 2 auch der Wert 2. Dies trifft bei linearen Funktionen zu.
Beispiel B: Verdoppelt man Größe 1, verdoppelt sich auch Größe 2. Dies trifft nur bei proportionalen Funktionen zu.
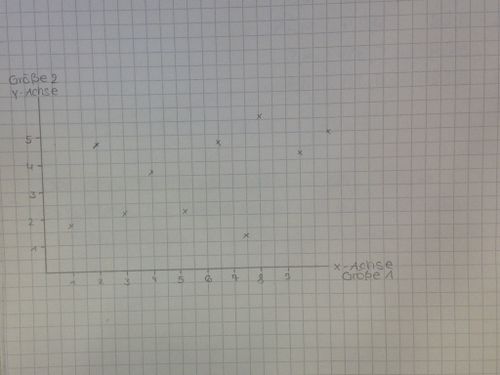
Nicht erkennbar als linearer Graph:
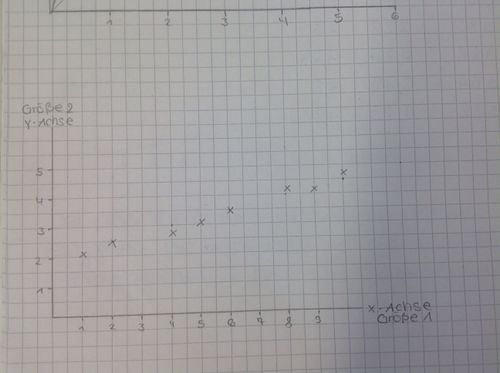
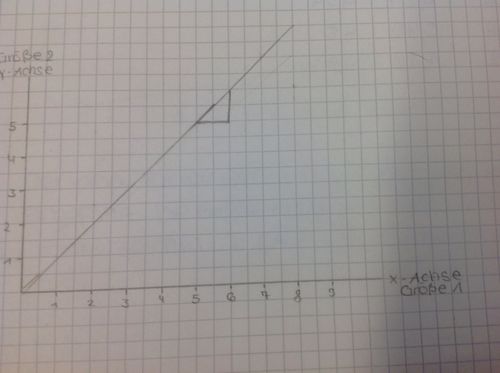
Beispiel für eine lineare Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 2 | 2,5 |
| 4 | 3 |
| 6 | 3,5 |
| 8 | 4 |
| 10 | 4,5 |
Eingezeichnete Punkte einer linearen Funktion:
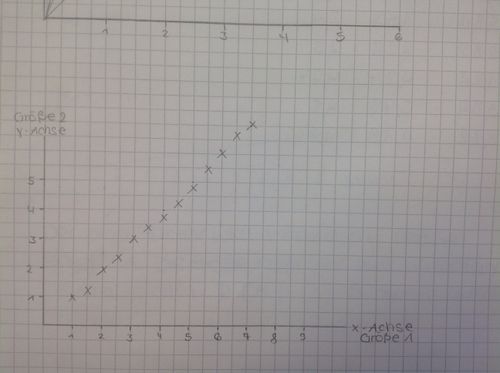
Beispiel für eine proportionale Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
Eingezeichnete Punkte einer proportionalen Funktion:
Zunächst wurden von uns zwei physikalische Größen gemessen, wobei wir bewusst eine Größe verändert und die andere gemessen haben, die Messwerte haben wir dann in eine Wertetabelle eingetragen. Die Größen haben wir danach in einem Koordiantensystem jeweils auf der x- und y-Achse eingezeichnet und nun werden Punkte im Koordinatensystem markiert, die den gemessenen Werten entsprechen. Dann wird ein Graph in Form einer Gerade gezogen. Falls man von einer proportionalen Funktion ausgeht, zieht man eine Gerade vom Nullpunkt aus, welche möglichst viele Messpunkte überschneidet, wobei sich die Steigung errechnen lässt, wenn man Wert x mit dem entsprechenden Wert y dividiert. Geht man jedoch von einer quadratischen Funktion aus, quadriert man die eine Größe und teilt sie durch die andere Größe, aus welcher sich die Steigung ergibt.
Daraufhin wird das Steigungsdreieck errechnet/abgelesen. Das Steigungsdreieck errechnet man, indem man schaut, um wie viel sich das y verändert, wenn sich x um eins erhöht. Die Steigung beschreibt, um wie viel der y-Wert pro x sich verändert.
Hierbei beträgt die Steigung 1, denn wenn x um 1 erhöht wird erhöht sich auch y um genau 1.
Daraus kann man den Funktionsterm y=mx bilden, wobei m für die Steigung des Graphen steht. Die neu entstandene physikalische Größe kann errechnet werden, indem man x durch y teilt.
Klasse 9b