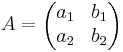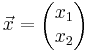Affine Abbildungen: Unterschied zwischen den Versionen
Aus KAS-Wiki
(Die Seite wurde neu angelegt: === Definition: === Eine geradentreue und umkehrbare geometrische Abbildung der Ebene auf sich selbst nennt man eine affine Abbildung oder Affinität. Die affine Ab...) |
|||
| Zeile 6: | Zeile 6: | ||
Die einzelnen Spalten der Matrix dürfen nicht linear abhängig sein. | Die einzelnen Spalten der Matrix dürfen nicht linear abhängig sein. | ||
| − | |||
| − | |||
<math>A=\begin{pmatrix} a_1 & b_1 \\ a_2 & b_2 \end{pmatrix}</math> | <math>A=\begin{pmatrix} a_1 & b_1 \\ a_2 & b_2 \end{pmatrix}</math> | ||
| Zeile 13: | Zeile 11: | ||
<math>\vec x=\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} | <math>\vec x=\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} | ||
</math> | </math> | ||
| + | |||
| + | <math>A*\vec x</math> | ||
Version vom 3. Dezember 2009, 11:27 Uhr
Definition:
Eine geradentreue und umkehrbare geometrische Abbildung der Ebene auf sich selbst nennt man eine affine Abbildung oder Affinität.
Die affine Abbildung bildet ein neues Koordinatensystem.
Die einzelnen Spalten der Matrix dürfen nicht linear abhängig sein.