Textaufgaben zu quadratischen Funktionen: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
K (typo)
 
Zeile 1: Zeile 1:
−
Bei Textaufgaben zu quadratischen Funktionen bearbeitet man Probleme die auf eine quadratische Gleichung führen. Die Informationen werden dabei aus einem meist knappen Text entnommen.
+
Bei Textaufgaben zu quadratischen Funktionen bearbeitet man Probleme, die auf eine quadratische Gleichung führen. Die Informationen werden dabei aus einem meist knappen Text entnommen.
  
  

Aktuelle Version vom 4. August 2010, 11:03 Uhr

Bei Textaufgaben zu quadratischen Funktionen bearbeitet man Probleme, die auf eine quadratische Gleichung führen. Die Informationen werden dabei aus einem meist knappen Text entnommen.


Inhaltsverzeichnis

Vorgehensweise

Aufgabenstellung

[ - Beispiel - ]

Die Aufgabenstellung beschreibt einen mathematischen Sachverhalt, der durch eine Zeichnung ergänzt sein kann. Es ist möglich, dass am Ende der Aufgabenstellung eine Frage steht, die konkret nach einer Antwort fragt. Ist dies nicht der Fall, muss sich der Leser selbst erschließen, was in der Aufgabe gesucht ist.


Bedingungen

[ - Beispiel - ]

Die Bedingungen kann man nach aufmerksamem Lesen aus der Aufgabenstellung und, falls Zeichnung vorhanden, auch aus dieser entnehmen.


Skizze zeichnen

[ - Beispiel - ]

Der Sachverhalt wird anhand einer Skizze dargestellt. Der Ursprungszustand und der veränderte Zustand müssen angegeben werden. Da es sich um eine Skizze handelt, muss der Sachverhalt nicht maßstabsgetreu wiedergegeben werden.


Beschriftung der Skizze

[ - Beispiel - ]

Als erstes wird das gesuchte "x" benannt und in der Skizze kenntlich gemacht.
Daraufhin werden die aus dem Text entnehmbaren Informationen in die Skizze übertragen. Wichtige unbekannte Größen werden mit Variablen (a,b,c...) gekennzeichnet. Bereits verwendete Variablen (wie z.B. x) dürfen für keine andere Strecke ungleich der schon zugeordneten Strecke verwendet werden.


Bedingungen festlegen

[ - Beispiel - ]

Die bisher in der Skizze bildlich veranschaulichten Bedingungen müssen nun als mathematische Gleichungen notiert werden.


Gleichung

[ - Beispiel - ]

Gleichung aufstellen

[ - Beispiel - ]

Die als Gleichungen notierten Bedingungen müssen ineinander eingesetzt werden. Dabei versucht man so zu ersetzen, dass zum Schluss eine Gleichung herauskommt, in der keine andere Variable als das gesuchte x vorkommt.


Gleichung lösen

[ - Beispiel - ]

Die gefundene Gleichung muss im folgenden gelöst werden.
Periodische Brüche und unendliche unperiodische Brüche dürfen nicht gerundet werden. Sie müssen weiterhin als Bruch, Wurzel, etc. geschrieben werden.


Lösungsmenge bestimmen

[ - Beispiel - ]

Die Lösungsmenge muss in folgender Form angegeben werden:

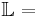
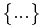
\mathbb L=\begin{Bmatrix}...\end{Bmatrix}

Gibt es zwei Lösungen, werden sie in der Lösungsklammer - durch ein Semikolon getrennt - der Größe nach geordnet.

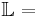
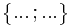
\mathbb L=\begin{Bmatrix}...\,;...\end{Bmatrix}


Probe

[ - Beispiel - ]

Probe der Gleichung

[ - Beispiel - ]

Die beiden Werte werden nacheinander in die zu lösende Gleichung eingesetzt.
Um nicht mit eventueller Punkt-vor-Strich-Rechnung oder sonstigem durcheinander zukommen, ist es sinnvoll die eingesetzten Lösungen in Klammern zu setzen.


Probe der Lösung in Bezug auf die Textaufgabe

[ - Beispiel - ]

Es wird getestet, ob die gefundenen Lösungen im Sachverhalt Sinn ergeben.


Ergebnis

[ - Beispiel - ]

Das Ergebnis muss in einem Antwortsatz formuliert werden. Dieser sollte möglichst treffend Antwort auf die Aufgabenstellung oder Frage liefern.



Beispiel

Aufgabenstellung (Bsp.)


Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.


Bedingungen (Bsp.)

Die Bedingungen kann man nach aufmerksamem Lesen aus der Aufgabenstellung entnehmen.

Skizze zeichnen (Bsp.)

Wichtige Informationen aus der Aufgaben stellung:

Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
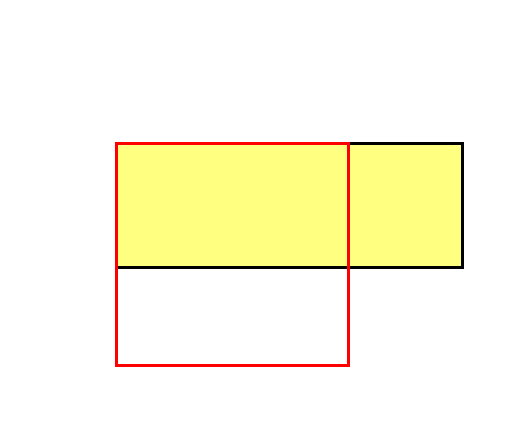
Skizze des gegebenen Sachverhalts












Zuerst skizziert man das Quadrat (rot). Der Aufgabenstellung nach wird darüber ein Rechteck (gelb) mit einer verlängerten und einer verkürzten Seite gezeichnet.















Beschriftung der Skizze (Bsp.)

Wichtige Informationen aus der Aufgabenstellung:

Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
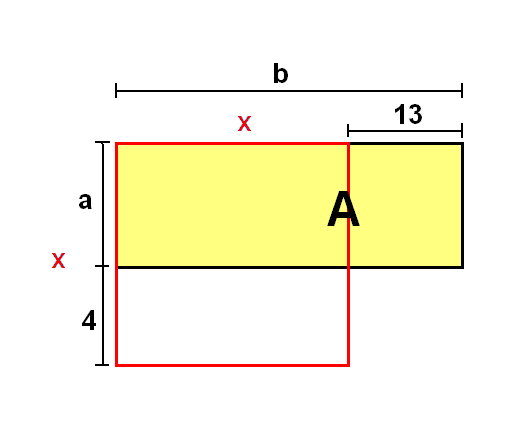
Skizze des gegebenen Sachverhalts mit Beschriftungen



  • Als erstes wird das gesuchte x bestimmt und kenntlich gemacht: die Seitenlänge des Quadrats.


  • Die um 4cm verkürzte Seite x wird mit der Variablen a gekennzeichnet.
  • Die um 13cm verlängerte Seite x wird mit der Variablen b gekennzeichnet.
(Variablen [a,b,c...] sind frei wählbar, die bereits verwendete Variable x darf jedoch für keine andere Strecke ungleich x erneut verwendet werden.)


  • Die beiden Variablen a und b stellen nun die Seiten des neuen Rechtecks A dar.



Bedingungen festlegen (Bsp.)


  • Aus diesen Bedingungen ergibt sich:


I. Gl.1

II. Gl.2

III. Gl.3


Wichtige Informationen aus der Aufgabenstellung:

Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.


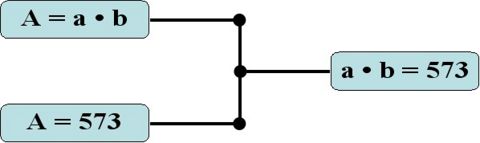
  • Aus der Aufgabenstellung lässt sich die Fläche von A (Rechteck) ableiten:


IV. Gl.4


Gleichung (Bsp.)

Gleichung aufstellen (Bsp.)


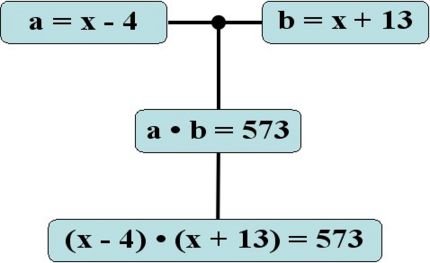
Nun können die bestehenden Gleichungen ineinander eingesetzt weden:


  • Gleichung I. in Gleichung IV.:


Gleichung 5.jpg V.


\rightarrow Resultat: Gleichung V.

Diese Gleichung wird im nächsten Schritt direkt weiter verwendet.




  • Gleichungen II. und III. in Gleichung V.:


Gleichung 6.jpg


\rightarrow Resultat: Gleichung VI.

Dies ist die gesuchte Gleichung.




Gleichung lösen (Bsp.)


  • Die gefundene Gleichung muss im Folgenden gelöst werden.


\begin{matrix} (x-4)(x+13)& = &573\\\\ x^2+13x-4x-52& = &573\\\\ x^2+9x-52& = &573 &&|\,quadratische\,Erg\ddot anzung\\\\ x^2+9x+20{,}25-20{,}25-52& = &573 &&|\,binomische\,Formel\\\\ (x+4{,}5)^2-20{,}25-52& = &573\\\\ (x+4{,}5)^2-72{,}25& = &573 &&|+72{,}25\\\\ (x+4{,}5)^2& = &645{,}25 &&|\sqrt{}\\\\ x_1+4{,}5=\sqrt{645{,}25}& v &x_2+4{,}5=-\sqrt{645{,}25} &&|-4{,}5\\\\ x_1=-4{,}5+\sqrt{645{,}25}& v &x_2=-4{,}5-\sqrt{645{,}25} \end{matrix}

Ausführliche Erläuterung:

  • Zeile 1: Klammern auflösen
  • Zeile 2: zusammenfassen
  • Zeile 3: quadratische Ergänzung
  • Zeile 4: binomische Formel
  • Zeile 5: zusammenfassen
  • Zeile 6: (+ 72,25)
  • Zeile 7: Wurzel ziehen (die Wurzel von 645,25 muss als "Wurzel von 645,25" notiert werden, da sonst Rundungsfehler zu Stande kommen.
Es müssen sowohl die positive als auch die negative Wurzel angegeben werden.
  • Zeile 8: (- 4,5)


Lösungsmenge bestimmen (Bsp.)


  • Die Werte werden in der Lösungsklammer der Größe nach geordnet. Das Semikolon zwischen den Werten dient zu Trennung.


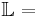
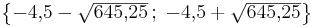
\mathbb L=\begin{Bmatrix}-4{,}5-\sqrt{645{,}25}\,;\;-4{,}5+\sqrt{645{,}25}\end{Bmatrix}

Probe (Bsp.)

Probe der Gleichung (Bsp.)


  • Die beiden Werte werden nacheinander in die zu lösende Gleichung eingesetzt.
  • Um nicht mit eventueller Punkt-vor-Strich-Rechnung oder sonstigem durcheinander zu kommen, ist es sinnvoll die eingesetzten Lösungen in Klammern zu setzen.


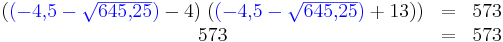
\begin{matrix} ({ \color{Blue}(-4{,}5-\sqrt{645{,}25}) }-4)\;({ \color{Blue}(-4{,}5-\sqrt{645{,}25}) }+13))&=&573\\ 573&=&573 \end{matrix}
  • Die Lösung ist richtig, da in der letzten Zeile die linke Seite gleich der rechten Seite ist.


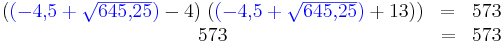
\begin{matrix} ({ \color{Blue}(-4{,}5+\sqrt{645{,}25}) }-4)\;({ \color{Blue}(-4{,}5+\sqrt{645{,}25}) }+13))&=&573\\ 573&=&573 \end{matrix}
  • Die Lösung ist richtig, da in der letzten Zeile die linke Seite gleich der rechten Seite ist.


Probe der Lösung in Bezug auf die Textaufgabe (Bsp.)


  • Nun wird getestet, ob die gefundenen Lösungen im Sachverhalt Sinn ergeben.


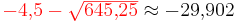
\begin{matrix} { \color{Red}-4{,}5-\sqrt{645{,}25}}\approx -29{,}902 \end{matrix} \rightarrow Diese Lösung kommt nicht in Frage, da es in der Geometrie keine Strecken kleiner Null gibt.

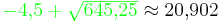
\begin{matrix} { \color{Green}-4{,}5+\sqrt{645{,}25}}\approx 20{,}902 \end{matrix} \rightarrow Diese Lösung macht im Sachverhalt Sinn, da keine Gegebenheiten widersprechen.

Ergebnis (Bsp.)


  • Das Ergebnis muss jetzt nur noch in einem Antwortsatz formuliert werden.


Antwort: Das ursprüngliche Quadrat hat eine Seitenlänge von ca. 20,902 cm.


Weblinks (Übungsaufgaben)

(Vorschläge erwünscht)

Von „http://kas.zum.de/index.php?title=Textaufgaben_zu_quadratischen_Funktionen&oldid=3920“