Textaufgaben zu quadratischen Funktionen: Unterschied zwischen den Versionen
| Zeile 141: | Zeile 141: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <math>\rightarrow</math> Resultat: Gleichung <big>'''V.'''</big> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | *Gleichungen <big>'''II.'''</big> und <big>'''III.'''</big> in Gleichung <big>'''V.'''</big>: | ||
| + | <br /> | ||
| + | [[Bild:Gleichung 6.jpg|430px]] | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>\rightarrow</math> Resultat: Gleichung <big>'''VI.'''</big> | ||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
Version vom 3. Dezember 2009, 20:50 Uhr
Bei Textaufgaben zu quadratischen Funktionen bearbeitet man Probleme die auf eine quadratische Gleichung führen. Die Informationen werden dabei aus einem meist knappen Text entnommen.
Inhaltsverzeichnis |
Vorgehensweise
Aufgabenstellung
Die Aufgabenstellung beschreibt einen mathematischen Sachverhalt, der durch eine Zeichnung ergänzt sein kann.
Bedingungen
Die Bedingungen kann man nach aufmerksamem Lesen aus der Aufgabenstellung und, falls Zeichnung vorhanden, auch aus dieser entnehmen.
Skizze zeichnen
Der Sachverhalt wird anhand einer Skizze dargestellt. Der Ursprungszustand und der veränderte Zustand müssen angegeben werden. Da es sich um eine Skizze handelt, muss der Sachverhalt nicht maßstabsgetreu wiedergegeben werden.
Beschriftung der Skizze
Als erstes wird das gesuchte "x" benannt und in der Skizze kenntlich gemacht.
Daraufhin werden die aus dem Text entnehmbaren Informationen in die Skizze übertragen. Wichtige unbekannte Größen werden mit Variablen (a,b,c...) gekennzeichnet. Bereits verwendete Variablen (wie z.B. x) dürfen für keine andere Strecke ungleich der schon zugeordneten Strecke verwendet werden.
Bedingungen festlegen
Die bisher in der Skizze bildlich veranschaulichten Bedingungen müssen nun als mathematische Gleichungen notiert werden.
Gleichung
Gleichung aufstellen
Gleichung lösen
Lösungsmenge bestimmen
Probe
Probe der Gleichung
Probe der Lösung in Bezug auf Textaufgabe
Ergebnis
Beispiel
Aufgabenstellung
Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
Bedingungen
Die Bedingungen kann man nach aufmerksamem Lesen aus der Aufgabenstellung entnehmen.
Skizze zeichnen
Wichtige Informationen aus der Aufgaben stellung:
Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
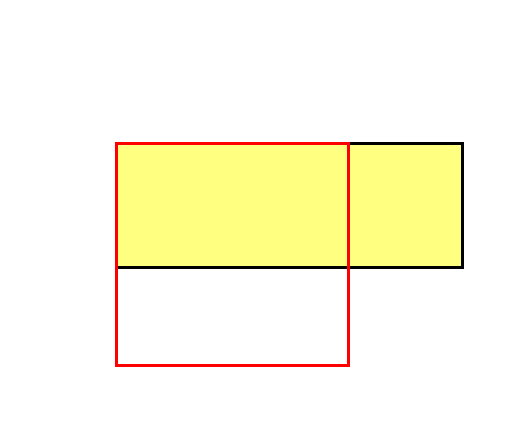
Zuerst skizziert man das Quadrat (rot). Der Aufgabenstellung nach wird darüber ein Rechteck (gelb) mit einer verlängerten und einer verkürzten Seite gezeichnet.
Beschriftung der Skizze
Wichtige Informationen aus der Aufgabenstellung:
Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
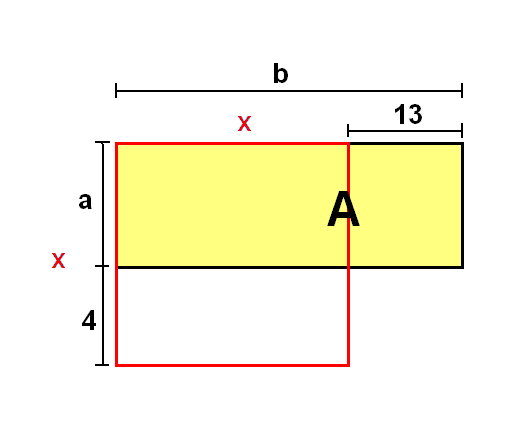
- Als erstes wird das gesuchte x bestimmt und kenntlich gemacht: die Seitenlänge des Quadrats.
- Die um 4cm verkürzte Seite x wird mit der Variablen a gekennzeichnet.
- Die um 13cm verlängerte Seite x wird mit der Variablen b gekennzeichnet.
- (Variablen [a,b,c...] sind frei wählbar, die bereits verwendete Variable x darf jedoch für keine andere Strecke ungleich x erneut verwendet werden.)
- Die beiden Variablen a und b stellen nun die Seiten des neuen Rechtecks A dar.
Bedingungen festlegen
- Aus diesen Bedingungen ergibt sich:
I. ![]()
II. ![]()
III. ![]()
Wichtige Informationen aus der Aufgabenstellung:
Verlängert man die eine Seite eines Quadrats um 13cm und verkürzt gleichzeitig die andere Seite um 4cm, so entsteht ein Rechteck mit einem Flächeninhalt von 573cm2.
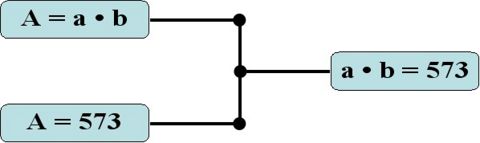
- Aus der Aufgabenstellung lässt sich die Fläche von A (Rechteck)ableiten:
Gleichung
Gleichung aufstellen
Nun können die bestehenden Gleichungen ineinander eingesetzt weden:
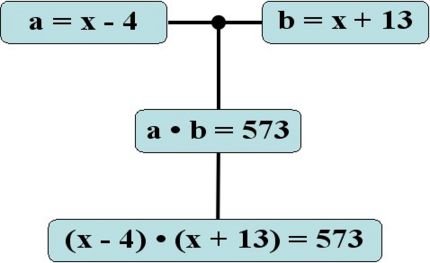
- Gleichung I. in Gleichung IV.:
- Gleichungen II. und III. in Gleichung V.:
Gleichung lösen
Lösungsmenge bestimmen
Probe
Probe der Gleichung
Probe der Lösung in Bezug auf Textaufgabe
Ergebnis
Tip
Textaufgaben sind echt manchmal schwer zu verstehen bzw die Gleichung herraus zu lesen. Hier ein paar Tipps um die "geheimsprache der Textaufgaben" herauszufinden.
Beispiel:(quelle arbeitsblatt in der vertretungsstunde-klapptest) Aufgabe1: Verlängert man eine Seite eines Quadrates um 5 cm und verkürtzt gleichzeitig die andere um 5cm, so entsteht ein Rechteck mit einem Flächeninhalt von 299cm².
so: ich makiere euch die hinweise: Unterstrichen bedeutet was "x" ist(unbestimmter Artikel)
Fett bedeutet + und - | Kursiv bedeutet das, was hinter dem = steht. Aufstellen der Gleichung: (x+5)(x-5)=299
jetzt müsst ihr nur noch die Gleichung lösen.
Lösung: L={-18|18} Antwortsatz: Die Seitenlänge des Quadrats beträgt 18cm.
Bei Fragen wendet euch doch an Herr Deeken oder zu diesem Thema an mich, Felix
 Resultat: Gleichung V.
Resultat: Gleichung V.