Und darauf ein kühles Bier!: Unterschied zwischen den Versionen
Emina1 (Diskussion | Beiträge) (Die Seite wurde neu angelegt: === Und darauf ein kühles Bier === Willi Fröhlich hat gerade eine Flasche Bier aus seinem <u>7°C kalten Kühlschrank</u> geholt, in dem sie schon seit zwei Tagen st...) |
Emina1 (Diskussion | Beiträge) (→Und darauf ein kühles Bier) |
||
| Zeile 6: | Zeile 6: | ||
'''b)''' Wie lange hätte die Dikussion mit Tante Frieda höchstens dauern dürfen, damit Willi sein Bier bereits nach 10 Minuten genüsslich trinken kann? | '''b)''' Wie lange hätte die Dikussion mit Tante Frieda höchstens dauern dürfen, damit Willi sein Bier bereits nach 10 Minuten genüsslich trinken kann? | ||
| + | |||
| + | ==Lösungen== | ||
| + | |||
| + | '''a)''' | ||
| + | |||
| + | Formel: <math>f(t) = S-c\cdot e^{-k\cdot t}</math> | ||
| + | |||
| + | S = 7. K = 10% = 0.1 | ||
| + | |||
| + | Beschräktes Wachstum, da der kühlschrank 7 | ||
Version vom 15. Februar 2011, 13:34 Uhr
Und darauf ein kühles Bier
Willi Fröhlich hat gerade eine Flasche Bier aus seinem 7°C kalten Kühlschrank geholt, in dem sie schon seit zwei Tagen stand. Als er sich das Bier genüsslich in sein Bierglas eingeschenkt hat, schellt es an der Tür und Tante Frieda verstrickt ihn ganze 90 Minuten lang in eine hitzige Diskussion über die Zukunft der Rentenversicherung. Derweil steht sein einsames Bier die ganze Zeit im Wohnzimmer, das der energiebewusste Willi auf einer Temperatur von 19°C hält. Kaum hat Willi die Haustür hinter Tante Frieda zugeschlagen, misst er, die Temperatur des Gerstensaftes und stellt eine betrübliche Überhitzung desselben auf 15°C fest. Akzeptabel wären für einen Biertrinker allenfalls 8°C.
a) Wie lange muss Willi sein Bier wieder in den Kühlschrank stellen, damit er es bei 8°C genüsslich trinken kann? Als erfahrener Biertrinker weiß Willi, dass im Kühlschrank sein Bier pro Minute um ca. 10% der noch vorhandenen Temperaturdifferenz zur Kühlschrankstemperatur abkühlt.
b) Wie lange hätte die Dikussion mit Tante Frieda höchstens dauern dürfen, damit Willi sein Bier bereits nach 10 Minuten genüsslich trinken kann?
Lösungen
a)
Formel: 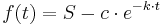
S = 7. K = 10% = 0.1
Beschräktes Wachstum, da der kühlschrank 7

