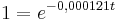Turiner Grabtuch: Unterschied zwischen den Versionen
Aus KAS-Wiki
Emina1 (Diskussion | Beiträge) (Die Seite wurde neu angelegt: == Turiner Grabtuch == === Aufgabe: === Im Jahr 1988 wurden Proben des Tuches genommen: * Zürich: ca.92,15% der ursprünglichen <sup>14</sup>C-Atome übrig * Oxford...) |
Giulia (Diskussion | Beiträge) (→Turiner Grabtuch) |
||
| Zeile 11: | Zeile 11: | ||
Halbwertszeit <math>T_H</math> von <sup>14</sup>C beträgt ca.5730 Jahre | Halbwertszeit <math>T_H</math> von <sup>14</sup>C beträgt ca.5730 Jahre | ||
| + | Frage: Wann entstand das Tuch? (Zu welcher Zeit waren noch 100% der <sup>14</sup>C-Atome vorhanden?) | ||
=== Lösung === | === Lösung === | ||
Version vom 15. Februar 2011, 12:43 Uhr
Turiner Grabtuch
Aufgabe:
Im Jahr 1988 wurden Proben des Tuches genommen:
- Zürich: ca.92,15% der ursprünglichen 14C-Atome übrig
- Oxford: ca.91,33% der ursprünglichen 14C-Atome übrig
- Arizona: ca.92,48% der ursprünglichen 14C-Atome übrig
Halbwertszeit 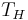 von 14C beträgt ca.5730 Jahre
von 14C beträgt ca.5730 Jahre
Frage: Wann entstand das Tuch? (Zu welcher Zeit waren noch 100% der 14C-Atome vorhanden?)
Lösung
Halbwertszeit: Zeit in der sich die Menge der Atome (Anfangswert) halbiert.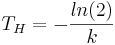
Nach k auflösen
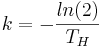
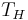 einsetzten in die Formel
einsetzten in die Formel
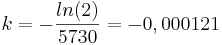
Es handelt sich um exponentiellen Zerfall, weil es keine Schranke gibt.
Formel des exponentiellen Zerfalls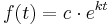
c ist der Anfangswert
k ist ist die Zerfallskonstante
t ist die Zeit in Jahren
Gesucht ist t zum Zeitpunkt als noch 100% der urspruenglichen 14C-Atome vorhanden sind