Flächenberechnung: Unterschied zwischen den Versionen
Giulia (Diskussion | Beiträge) (→Flächeninhalt A zwischen dem Graphen f und der x-Achse) |
Giulia (Diskussion | Beiträge) (→Flächeninhalt A zwischen dem Graphen f und der x-Achse) |
||
| Zeile 57: | Zeile 57: | ||
1.) Nullstellen berechnen --> f(x)=0 | 1.) Nullstellen berechnen --> f(x)=0 | ||
| − | + | \begin{matrix} | |
| − | + | 0,5x^3-2x&=& 0 \\ | |
| − | x(0,5x^2-2)=0 | + | \ x(0,5x^2-2)& =& 0 \\ |
| − | + | \ x=0; 0,5x^2-2& =& 0 \\ | |
| − | x=0 ; 0,5x^2-2=0 | + | \ x=2 und x& =& -2 |
| + | \end{matrix} | ||
Version vom 1. Mai 2011, 14:06 Uhr
Flächeninhalt A zwischen dem Graphen f und der x-Achse
Für den Inhalt A der Fläche zwischen dem Graphen f und der x-Achse über [a,b] gilt:
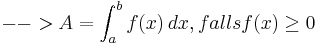
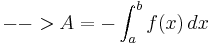
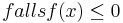
denn: Das Integral zählt Flächeninhalte oberhalb der x-Achse positiv und unterhalb der x-Achse negativ.
Beispielaufgaben:
Beispiel 1: Fläche oberhalb der x-Achse
--> Berechnen Sie den Inhalt der gefärbten Fläche in Fig.1.
Lösung: Da 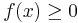 für
für ![x\in\ [-1,1]](/images/math/b/8/c/b8c773b6de0758bb1167e2bb6d2b0569.png) ist, gilt:
ist, gilt:
![A=\int_{1-}^{1} x^2\, dx= [\frac{1}{3}x^3]
= \frac{1}{3} \cdot 1^3-\frac{1}{3} \cdot (-1)^3= \frac{1}{3}-(-\frac{1}{3})= \frac{2}{3}](/images/math/c/e/3/ce3fb92ea679f57b69072e193ffff83a.png)
Der Flächeninhalt beträgt 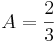
Beispiel 2: Fläche unterhalb der x-Achse
--> Berechnen Sie den Inhalt der gefärbten Fläche in Fig.2.
Lösung: Da 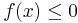 für
für ![x\in\ [-1,3]](/images/math/4/d/0/4d0017cb5d984bbac3d4692906648585.png) ist, gilt:
ist, gilt:
![A=-\int_{-1}^{3} -\frac{1}{4}x^2\, dx=\int_{-1}^{3} \frac{1}{4}x^2\, dx= [\frac{1}{12}x^3]= \frac{1}{12} \cdot 3^3-\frac{1}{12} \cdot (-1)^3= -\frac{9}{4}-(-\frac{1}{12})= \frac{7}{3}](/images/math/4/b/d/4bd409b55c1295780fe04a9e78f37454.png)
Der Flächeninhalt beträgt A= Der Flächeninhalt beträgt 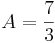
Sollte f in [a,b] jedoch sowohl oberhalb als auch unterhalb der x-Achse verlaufen, so muss man die Inhalte der Teilflächen getrennt berechnen:
1.) Berechnung der Nullstellen von f
2.) Bestimmung des Vorzeichens von f(x) oder ggf. Betragsstriche um die jeweiligen Teilflächen setzen
3.) Berechnung des gesamten Flächeninhalts, indem man die einzelnen Teilflächen miteinander addiert.
Beispielaufgabe:
Beispiel3: Fläche teilweise oberhalb und teilweise unterhalb der x-Achse
Gegeben ist die Funktion f mit f(x)= 0,5x^3-2x (Fig.3).
Berechnen Sie den Inhalt der Fläche, die der Graph von f und die x-Achse über dem Intervall [-1;2,5] einschließen.
Lösung:
1.) Nullstellen berechnen --> f(x)=0
\begin{matrix} 0,5x^3-2x&=& 0 \\ \ x(0,5x^2-2)& =& 0 \\ \ x=0; 0,5x^2-2& =& 0 \\ \ x=2 und x& =& -2 \end{matrix}

