Die gleichförmige Bewegung: Unterschied zwischen den Versionen
Aus KAS-Wiki
(→Aufgaben) |
(→Aufgaben) |
||
| Zeile 33: | Zeile 33: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | Graph (Aufgabe 2,6): | + | '''<u>Graph (Aufgabe 2,6):</u>''' |
| − | Aufgabe 3: | + | <u>'''Aufgabe 3:'''</u> |
1,0 : 0,015 = 66,66666667 | 1,0 : 0,015 = 66,66666667 | ||
| Zeile 46: | Zeile 46: | ||
| − | Aufgabe 4: | + | <u>'''Aufgabe 4:'''</u> |
Für uns bedeutet x:t die Ortskoordinate geteilt durch die Zeit. | Für uns bedeutet x:t die Ortskoordinate geteilt durch die Zeit. | ||
| − | Aufgabe 5: | + | <u>'''Aufgabe 5:'''</u> |
Uns fällt auf, dass es immer einen Zeitunterschied von 0,2 sec gibt. | Uns fällt auf, dass es immer einen Zeitunterschied von 0,2 sec gibt. | ||
| − | Aufgabe 7: | + | <u>'''Aufgabe 7:'''</u> |
Eine Bewegung heißt gleichförmig, wenn sie gradlinig verläuft und wenn in gleichen Zeitabschnitten <math>\delta t</math> die gleichen Wegabschnitte <math>\delta s</math> zurücklegt. | Eine Bewegung heißt gleichförmig, wenn sie gradlinig verläuft und wenn in gleichen Zeitabschnitten <math>\delta t</math> die gleichen Wegabschnitte <math>\delta s</math> zurücklegt. | ||
Version vom 15. Juni 2011, 08:53 Uhr
| Zeit in ms |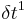 
|
|
|
|---|---|---|---|
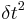
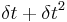
| 1. Bewegung | 0,020 | 0,684 | 0,752 |
| 2. Bewegung | 0,015 | 0,414 | 0,438 |
| 3. Bewegung | 0,011 | 0,309 | 0,325 |
| Ortskoordinate x in cm | 1,0 | 20,0 | 21,0 |
| Zusammenhang von x und t | 67 | 48 | 48 |
Aufgaben
Graph (Aufgabe 2,6):
Aufgabe 3:
1,0 : 0,015 = 66,66666667
20,0 : 0,414 = 48,30917874
21,0 : 0,438 = 47,94520548
(Zusammenhang in der Tabelle)
Aufgabe 4:
Für uns bedeutet x:t die Ortskoordinate geteilt durch die Zeit.
Aufgabe 5:
Uns fällt auf, dass es immer einen Zeitunterschied von 0,2 sec gibt.
Aufgabe 7:
Eine Bewegung heißt gleichförmig, wenn sie gradlinig verläuft und wenn in gleichen Zeitabschnitten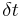 
die gleichen Wegabschnitte 
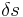zurücklegt.
