Elementare Integration.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Gamze1 (Diskussion | Beiträge) |
Gamze1 (Diskussion | Beiträge) |
||
| Zeile 57: | Zeile 57: | ||
<br /> | <br /> | ||
== Integralrechnung == | == Integralrechnung == | ||
| − | + | Mit einer beliebigen Stammfunktion F(x) von f(x) kann man den gesuchten Flächeninhalt berechnen. | |
| − | '''Hauptsatz der Differenzial- und Integralrechnung''' | + | <br />'''Hauptsatz der Differenzial- und Integralrechnung''' |
| + | <math>\int_{b}^{a} f(x) \, dx</math> = F(b) - F(a) | ||
Version vom 14. Dezember 2009, 11:10 Uhr
Elementare Integration
Durch integrieren werden die Flächen unterhalb oder zwischen den Graphen berechnet. Dazu muss man zuerst die gegebene Funktion aufleiten bzw. die Stammfunktion bilden.
Stammfunktionen bilden
Wenn man eine Funktion f(x) gegeben hat, ist ihre Stammfunktion die Funktion, deren Ableitung f ergibt.
F'(x) = f(x)
Die Stammfunktion f(x) wird gebildet, indem man den Exponenten mit eins addiert und die Funktion mit dem Kehrwert des neuen Exponenten multipliziert.
| Funktion f (x) | Stammfunktion F(x) |
|---|---|
| f(x) = xz | F(x) =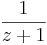 x z + 1 x z + 1
|
Beispiele:
f(x) = 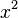 |
F(x) = 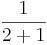 x 2 + 1 x 2 + 1 |
F(x) =  x 3 x 3
|
f(x) = 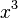 |
F(x) = 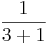 x 3 + 1 x 3 + 1 |
F(x) =  x 4 x 4
|
| f(x) = 4x + 1 | F(x) = 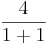 x 1 + 1 + 1 x 1 + 1 + 1 |
F(x) = 2 x 2 + x |
Bei Funktionen wie z.B. : (2x-3)3 erfolgt die Stammfunktionsbildung mit linearer Substitution.
| Funktion f(x) | Stammfunktion F(x) |
|---|---|
| f(x) = u(rx+s) | F(x) = 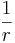 U (rx + s) U (rx + s)
|
Beispiele:
| f(x) = (4x+1)3 | F(x) =  * *  (4x + 1) 4 (4x + 1) 4 |
F(x) = 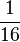 (4x + 1) 4 (4x + 1) 4
|
| f(x) = 2(x + 3)3 | 2 *  * *  (x + 3) 4 (x + 3) 4 |
F(x) =  (x + 3) 4 (x + 3) 4
|
Integralrechnung
Mit einer beliebigen Stammfunktion F(x) von f(x) kann man den gesuchten Flächeninhalt berechnen.
Hauptsatz der Differenzial- und Integralrechnung= F(b) - F(a)

