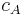Nernst-Gleichung: Unterschied zwischen den Versionen
(→Herleitung der Nernst-Gleichung) |
|||
| Zeile 32: | Zeile 32: | ||
<br /> | <br /> | ||
<math> U = 0,059 V\lg\frac{c_{A}(Ag^{+})}{c_{D}(Ag^{+})} </math> | <math> U = 0,059 V\lg\frac{c_{A}(Ag^{+})}{c_{D}(Ag^{+})} </math> | ||
| + | <br /> | ||
| + | wobei <math>c_A</math> | ||
Version vom 14. Dezember 2009, 16:55 Uhr
Die Nernst-Gleichung beschreibt den Einfluss der Konzentration auf das Potential eines Redoxsystems.
Allgemein lässt sich die Nernst-Gleichung wie folgt formulieren:
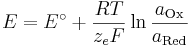
Unter Standardbedingungen vereinfacht sich die Nernst-Gleichung und man betrachtet nur noch die Abhängigkeit von der Konzentration.
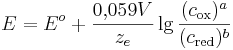
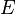Elektrodenpotential
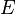° Standardelektronenpotential
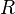molare Gaskonstante
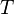Temperatur in Kelvin
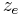Anzahl der übertragenen Elektronen
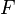Faraday-Konstante
Herleitung der Nernst-Gleichung
Am Beispiel einer Konzentrationszelle aus einer Standard-Silber-Halbzelle und einer Silberhalbzelle mit unterschiedlichen Konzentrationen lässt sich die Nernst-Gleichung in einfacher Form ableiten.
Variiert man nämlich die Konzentration der Nicht-Standard-Silberzelle und misst die resultierende Spannung, kann man die Messreihe mit Hilfe der Logarithmus-Funktion linearisieren:
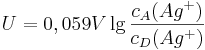
wobei 
