Turiner Grabtuch

Turiner Grabtuch

Aufgabe:

Im Jahr 1988 wurden Proben des Tuches genommen:

• Zürich: ca.92,15% der ursprünglichen ¹⁴C-Atome übrig
• Oxford: ca.91,33% der ursprünglichen ¹⁴C-Atome übrig
• Arizona: ca.92,48% der ursprünglichen ¹⁴C-Atome übrig

Halbwertszeit 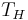$T_H$ von ¹⁴C beträgt ca.5730 Jahre

Frage: Wann entstand das Tuch? (Zu welcher Zeit waren noch 100% der ¹⁴C-Atome vorhanden?)

Lösung

Halbwertszeit: Zeit in der sich die Menge der Atome (Anfangswert) halbiert.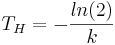
$T_H=-\frac{ln(2)}{k}$

Nach k auflösen $k=-\frac{ln(2)}{T_H}$

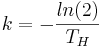
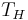$T_H$ einsetzten in die Formel $k=-\frac{ln(2)}{5730}=-0,000121$

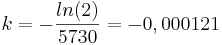
Die Halbwertszeit beträgt 5730 Jahre, das heißt für die Änderungsrate, dass sich in 5730 Jahren die Anzahl der ¹⁴C-Atome um die Hälfte der ursprünglichen Anzahl verringert.

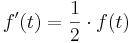$f'(t)=\frac{1}{2}\cdot f(t)$ (1t entspricht 5730 Jahren)

$f'(t)=-0,00012\cdot f(t)$

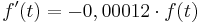
Es handelt sich um exponentiellen Zerfall, weil es keine Schranke gibt.

Formel des exponentiellen Zerfalls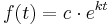 
$f(t)=c\cdot e^{kt}$

c ist der Anfangswert

k ist ist die Zerfallskonstante

t ist die Zeit in Jahren

Gesucht ist t zum Zeitpunkt als noch 100% der urspruenglichen ¹⁴C-Atome vorhanden sind

$1\cdot c=c\cdot e^{-0,000121t}$
$1=e^{-0,000121t}$