Gebrochene rationale Funktionen.
Inhaltsverzeichnis |
Defition von gebrochenrationalen Funktionen
Eine gebrochenrationale Funtion ist ein Bruch zweier ganzrationaler Funtionen g(x) und h(x). Dabei heißt g(x) Zählerfunktion mit dem Zählergrad ZG und h(x) heißt Nennerfunktion mit dem Nennergrad NG.
Allgemeine Form der Funktion: 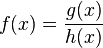 mit dem ganzrationalen Funktionen
g(x) und h(x) ( Grad h(x)
mit dem ganzrationalen Funktionen
g(x) und h(x) ( Grad h(x) 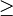 1).
1).
Bei einer ganzrationalen ist der Funktionsterm ein Polynom.
Ist z.B. g(x) = 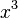 + x und
+ x und 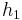 (x) =
(x) = 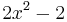 , ergibt sich
, ergibt sich 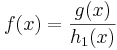 =
=
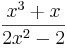 =
= 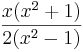 .
.
Diese Art von Funktionen nennt man gebrochenrationale Funktion.
Ist dagegen 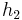 =
= 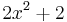 , ergibt sich
, ergibt sich 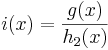 =
= 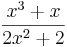 =
= 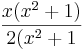 =
=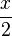 .
.
Durch das Kürzen ändert sich in diesem Fall die Definitionsmende nicht. Es ergibt sich als Nennerpolynom eine Konstante. Die Funktion i ist also ein ganzrationale Funktion.
Damit kann man formulieren:
Eine Funktion f mit 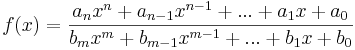 ,
, 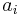
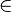
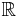 ,
, 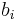
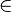
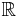 ,
, 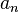
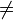 0 ,
0 , 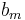
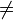 0, heißt gebrochenrational, wenn diese Darstellung nur mit einem Nennerpolynom möglich ist, dessen Grad mindestens 1 ist.
0, heißt gebrochenrational, wenn diese Darstellung nur mit einem Nennerpolynom möglich ist, dessen Grad mindestens 1 ist.
Falls das Nennerpolynom den Grad 0 hat, ist f eine ganzrationale Funktion.
Definitionsmenge
Nenner = 0 setzen
y-Achsenabschnitt
x = 0 setzen, f(0)= ...
Nullstellen und Polstellen
Um einen Überblick über den Verlauf des Graphen einer gebrochenrationalen Funktion f mit 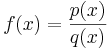 zu gewinnen, untersucht man f zunächst auf Nullstellen des Zählers und auf Definitionslücken.
zu gewinnen, untersucht man f zunächst auf Nullstellen des Zählers und auf Definitionslücken.
Nullstellen
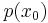 = 0 und
= 0 und 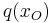
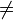 0
0
Zähler = 0 setzen
Beispiel 1:
Bei der Funktion 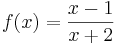 ist an der Stelle
ist an der Stelle 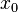 = 1 der Zähler null und der Nenner ungleich null.
= 1 der Zähler null und der Nenner ungleich null. 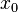 ist die Nullstelle der gebrochenrationalen Funktion f.
ist die Nullstelle der gebrochenrationalen Funktion f.
Polstelle
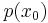
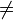 0 und
0 und 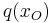 = 0
= 0
Nenner = 0 setzen
Beispiel 2:
Bei der Funktion 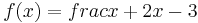 ist an der Stelle
ist an der Stelle 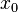 = 3 der Zähler ungleich null und der Nenner null.
= 3 der Zähler ungleich null und der Nenner null. 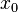 ist Pollstelle der der gebrochenrationalen Funktion f.
ist Pollstelle der der gebrochenrationalen Funktion f.
Hebbare Definitionslücke
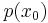 = 0 und
= 0 und 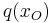 = 0
= 0
Zähler und Nenner = 0
Beispiel 3:
Bei der Funktion 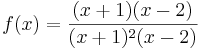 ; D =
; D = 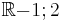 sind an der Stelle
sind an der Stelle 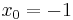 und
und 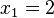 sowohl der Nenner als auch der Zähler gleich null. Nach dem Kürzen gilt:
sowohl der Nenner als auch der Zähler gleich null. Nach dem Kürzen gilt:
Für alle x 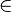 D ist
D ist 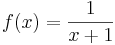 und damit Fehler beim Parsen(Lexikalischer Fehler): \ lim _ {x \to \2}
und damit Fehler beim Parsen(Lexikalischer Fehler): \ lim _ {x \to \2}
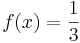 ;
; 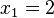 ist keine Polstelle ; dort ist eine hebbare Definitionslücke.
ist keine Polstelle ; dort ist eine hebbare Definitionslücke.
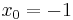 ist eine Polstelle. An der Stelle
ist eine Polstelle. An der Stelle 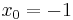 hat der Graph eine senkrechte Asymptote, der Punkt P ( 2 /
hat der Graph eine senkrechte Asymptote, der Punkt P ( 2 /  ) gehört nicht zum Graphen der Funktion f.
) gehört nicht zum Graphen der Funktion f.
Polstelle mit und ohne Vorzeichenwechsel
In der Umgebung einer Polstelle zeigen gebrochenrationale Funktionen unterschiedliches Verhalten.
Beispiel 1:
Die Funktion f mit 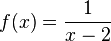 an der Stelle
an der Stelle 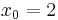 eine Polstelle.
Bei linksseitiger Annäherung an
eine Polstelle.
Bei linksseitiger Annäherung an 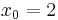 werden Funktionswerte beliebig klein; bei rechtsseitiger Annäherung beliebig groß.
werden Funktionswerte beliebig klein; bei rechtsseitiger Annäherung beliebig groß.
Man schreibt:
Für x --> 2 und x 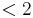 gilt: f(x) --> -
gilt: f(x) --> - 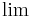 ,
,
für x --> 2 und x 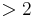 gilt: f(x) --> +
gilt: f(x) --> + 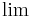
Man sagt: Die Funktion f hat an der Stelle 2 eine Polstelle mit Vorzeichenwechsel (VZW) von - nach +. Der Graph nähert sich von links und von rechts der Geraden mit der Gleichung x = 2 beliebig genau an.
Beispiel 2:
Die Funktion g mit 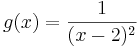 hat an der Stelle
hat an der Stelle 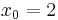 ebenfalls eine Polstelle.
Für x --> 2 gilt aber g(x) --> +
ebenfalls eine Polstelle.
Für x --> 2 gilt aber g(x) --> + 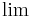 sowohl für x
sowohl für x 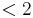 als auch für x
als auch für x 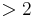 .
.
Man sagt: Die Funktion g hat an der Stelle 2 eine Polstelle ohne VZW. Auch der Graph von g nähert sich von links und vo rechts der Geraden mit der Gleichung x = 2 beliebig genau an.
IstPolstelle einer gebrochenrationalen Funktion so gilt:
--> +
für x -->
Die Gerade mit der Gleichung
heißt senkrechte Asymptote des Graphen von f.
Verhalten im Unendlichen, Näherungsfunktionen
Das " Grenzverhalten " einer gebrochenrationalen Funktion f mit 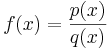 hängt vom Grad n des Zählerpolynoms p(x) und vom Grad m des Nennerpolynoms q(x) ab.
hängt vom Grad n des Zählerpolynoms p(x) und vom Grad m des Nennerpolynoms q(x) ab.
1. Fall : 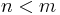
Für f mit 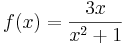 ist n = 1 und m = 2.
ist n = 1 und m = 2.
Da für x --> 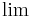 sowohl p(x) als auch q(x) gegen unendlich streben, formt man um. Division von p(x) als auch q(x)
durch x
sowohl p(x) als auch q(x) gegen unendlich streben, formt man um. Division von p(x) als auch q(x)
durch x 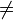 0 ergibt:
0 ergibt:
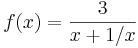 in
in 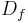
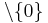 .
.
Jetzt erkennt man: lim f(x) = 0.
Die x-Achse ist eine waagerechte Asymptote mit der Gleichung y = 0.
2.Fall: n = m
Für f mit der Funktion 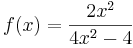 ist n = m = 2.
ist n = m = 2.
Division des Zählers und des Nenners durch 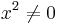 ergibt:
ergibt: 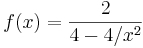 in
in
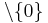 .
.
Man erkennt: lim 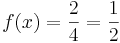 .
.
Die Gerade mit der Gleichung y =  ist eine waagerechte Asymptote.
ist eine waagerechte Asymptote.
3. Fall: n = m + 1
Für f mit 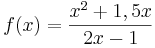 ist n = 2 und m = 1. Division des Zählers und des Nenners durch
ist n = 2 und m = 1. Division des Zählers und des Nenners durch
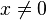 ergibt:
ergibt: 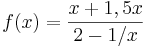 .
Für x --> +
.
Für x --> + 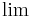 gilt somit: f(x) --> +
gilt somit: f(x) --> + 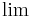 . Genauere Auskunft über das Verhalten der Funktionswerte
von f für x --> +/-
. Genauere Auskunft über das Verhalten der Funktionswerte
von f für x --> +/- 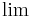 erhält man, wenn man das Zählerpolynom durch das Nennerpolynom dividiert --> Polynomdivision
erhält man, wenn man das Zählerpolynom durch das Nennerpolynom dividiert --> Polynomdivision
(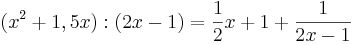
Für x --> +/- 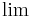 unterscheiden sich die Funktionswerte von f beliebig wenig von denen der Fuktion g mit
unterscheiden sich die Funktionswerte von f beliebig wenig von denen der Fuktion g mit
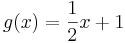 . Der Graph von g ist eine schiefe Asymptote
. Der Graph von g ist eine schiefe Asymptote
4.Fall: n > m + 1
Für f mit 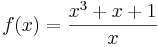 ist n=3 und m=1 ;
f(x) =
ist n=3 und m=1 ;
f(x) = 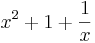 ;
; 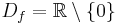 .
.
Der Anteil 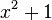 ist nicht linear. Die Funktion g mit
ist nicht linear. Die Funktion g mit 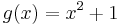 heißt ganzrationale Näherungsfunktion, der Graph mit der Gleichung
heißt ganzrationale Näherungsfunktion, der Graph mit der Gleichung 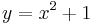 heißt Näherungsparabel.
heißt Näherungsparabel.
Allgemein spricht man auch von einer Näherungskurve für 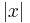 --> unendlich
--> unendlich
Symmetrie
a) Achsensymmetrie zur y- Achse
Bed. f(-x) = f(x)
b) Punktsymmetrie zum Ursprung
Bed. - f(-x) = f(x)
Ableitungen
Extremstellen

