Kurvendiskussion von Funktionsscharen

Kurvendiskussion an der Funktionsschar: 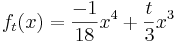$f_t(x)=\frac{-1}{18}x^4+\frac{t}{3}x^3$

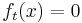
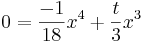
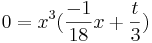
Nullstellen: $f_t(x)=0$

             $0=\frac{-1}{18}x^4+\frac{t}{3}x^3$
             $0=x^3(\frac{-1}{18}x+\frac{t}{3})$
             $\frac{-1}{18}x+\frac{t}{3}=0$    v    $x^3=0$ => x1=0
             $\frac{-t}{3}=\frac{-1}{18}x_2$
             $6t=x_2$

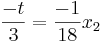
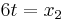
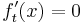
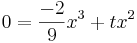
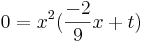
Extremstellen: $f_t'(x)=0$

              $0=\frac{-2}{9}x^3+tx^2$
              $0=x^2(\frac{-2}{9}x+t)$  
              $0=\frac{-2}{9}x+t$   v    $0=x^2$   =>  x1=0
              $x_2=\frac{9}{2}t$

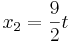
Zu prüfen ist: 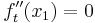$f_t''(x_1)=0$ => Sattelpunkt