Ziehen mit Reihenfolge mit Zurücklegen.

Das "Ziehen mit Reihenfolge mit Zurücklegen" oder Variation mit Zurücklegen

Wenn aus n Objekten k Objekte mit Zurücklegen und mit Beachtung der Reihenfolge ausgewählt werden sollen, dann kann jedes der n Objekte auf jedem der k Plätze der Auswahl erscheinen, es gibt demzufolge

• n^k mögliche Auswahlen.

Mengendarstellung: Die Menge 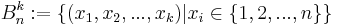$B_n^k := \{(x_1, x_2, ..., x_{k}) | x_{i} \in \{1, 2, ..., n\} \}$ ist die Menge aller Variationen mit Wiederholung von n Dingen zur Klasse k (für 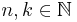$n, k \in \mathbb{N}$). Sie heißt auch Menge aller Permutationen mit Wiederholung von n Dingen zur Klasse k. Sie hat die oben angegebene Anzahl von Elementen.

Beispiel

• Wenn aus 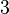$3$ Objekten 11 mal mit Zurücklegen gezogen wird, dann sind 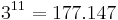$3^{11} = 177.147$ verschiedene Auswahlen möglich.
• Beispiel Zahlenschloss: Bei einem Zahlenschloss mit 3 Ringen und je 10 Ziffern gibt es 103 = 1000 verschiedene Variationen (000 - 999).
• Beispiel aus Digitaltechnik: Eine Binärzahl kennt 2 Zustände (0 und 1). Mit einer Reihenfolge von x Zahlen können 2x verschiedene Variationen entstehen. Eine vierstellige Binärzahl hat somit 24 = 16 verschiedene Zustände.