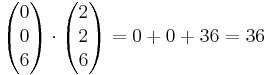Spatprodukt.
Aus KAS-Wiki
Version vom 17. Dezember 2010, 11:23 Uhr von Meric K. (Diskussion | Beiträge)
Mit dem Spatprodukt berechnet man das Volumen eines durch drei Vektoren aufgespannten Spats.
Die allgemeine Formel lautet: 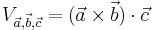
Beispiel 1
Berechne das Volumen des Spat, das durch die Vektoren 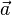 =
=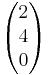 ,
, 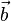 =
= 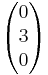 und
und  =
= 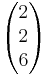
Also 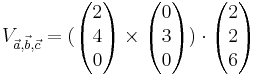 =
=