Schnittwinkel.
Dieser Artikel beschreibt den Vorgan der Schnittpunkt- und Schnittwinkel bestimmung.
Inhaltsverzeichnis |
Schnittpunkt zweier Gerdaden
Beispiel: 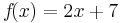
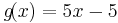
1.) Beide Funktionen gleichsetzten und nach x auflösen
Beispiel: 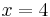
2.) Nun x in einer der beiden Gleichungen einsetzten und y bestimmen.
Beispiel: 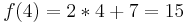
3.) x und y Stellen die Koordinaten des Schnittpunkt dar 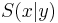 .
.
Beispiel: 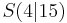
Schnittpunkt mit der x-Achse
Beispiel: 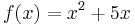
1.) Die Gleichung 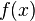 gleich 0 setzten.
gleich 0 setzten.
Beispiel: 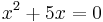
2.) Die Gleichung 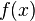 nach x auflösen.
nach x auflösen.
Beispiel: 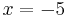
3.) Der x-Wert ist die Nullstelle 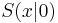 .
.
Beispiel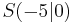
Schnittpunkte mit der y-Achse
Beispiel: 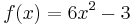
1.) x gleich 0 setzten.
Beispiel: 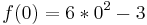
2.) Gleichung nach y auflösen.
Beispiel: 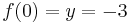
3.) y ist der y-Wert des Schnittpunktes 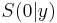
Beispiel: 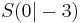
Schnittwinkel an Nullstellen
Beispiel: 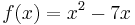
1.) Bilden sie die erste Ableitung von 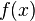 .
.
Beispiel: 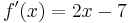
2.) 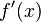 gleich 0 setzten.
gleich 0 setzten.
Beispiel: 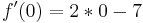
Schnittwinkel an zwei Geraden
Schnittwinkel zwischen Geraden und Ebene
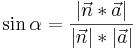
Dabei ist 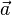 der Richtungsvektor der Geraden und
der Richtungsvektor der Geraden und 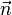 der Normalenvektor der Ebene.
der Normalenvektor der Ebene.
Schnittwinkel zwischen zwei Ebenen
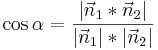
Dabei ist 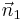 der Normalenvektor der ersten Ebene und
der Normalenvektor der ersten Ebene und 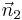 der Normalenvektor der zweiten Ebene.
der Normalenvektor der zweiten Ebene.

