BAM

Mikroskop

Wie funktioniert ein Mikroskop?

Mikroskope können sehr kleine Dinge vergrößern. Dies funktioniert nur mit Licht. Das Licht wird von der Lichtquelle am Fuß des Mikroskops ausgestrahlt und mit Hilfe von Linsen gebrochen, das heißt, dass das Licht in eine bestimmte Richtung gelenkt wird. Das Licht durchdringt das Objekt, das auf dem Objektträger liegt, welches auf dem Objekttisch gespannt ist. Dann wird das Licht in den Tubus geleitet, wo ein vergrößertes "reeles Zwischenbild", quasi ein Zwischenschritt Der gesamten Vergrößerung, ensteht.

Aufbau eines Mikroskops

Quelle: www.lichtmikroskop.net

Wie funktioniert eine Sammellinse?

Eine Sammellinse ist gewölbt und in der Mitte dicker als am Rand. Sie kann Licht bündeln. Mann nennt sie auch Konvexlinse oder Positivlinse, da sie eine Positive Brechkraft hat. Parrallel einfallendes Licht wird von der Sammellinse in einem Brennpunkt hinter der Linse gebündelt. Man sagt auch, dass das Licht im Brennpunkt fokussiert wird.

Formel für die Brennweite der Sammellinse:

1 1 1 - = - + - f g b

f ist die Brennweite (der Abstand des Brennpunktes vom Linsenmittelpunkt)

g ist die Gegenstandsweite (wie weit der Gegenstand vom Linsemittelpunkt entfernt ist)

b ist die Bildweite (der Abstand vom entstehenden Bild zum Linsenmittelpunkt)

Wie funktioniert eine Zerstreungslinse?

Eine Zerstreeungslinse nennt man auch Konkavlinse und ist in der Mitte dünner als am Rand. Anders als bei der Konvexlinse wird parallel einfallendes Licht zerstreut anstatt gebündelt. Die Zerstreungslinse hat auch einen Brennpunkt, der allerdings vor der Linse ist und nicht wie bei der Konvexlinse dahinter.

Formel für die Brennweite der Konkavlinse:

$\frac{1}{b}+\frac{1}{g}=\frac{1}{f}$

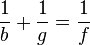
f ist die Brennweite (der Abstand des Brennpunktes vom Linsenmittelpunkt)

g ist die Gegenstandsweite (wie weit der Gegenstand vom Linsemittelpunkt entfernt ist)

b ist die Bildweite (der Abstand vom entstehenden Bild zum Linsenmittelpunkt)

Experimente

Brechen von Licht

Ohne das Brechen von Licht würde das Mikroskop nicht funktionieren, da das Licht von der Lichquelle dann einfach immer größer werden würde und nicht den Weg "langfließen" würde, wo es hinmuss, sodass das Mikroskop funktioniert. Das Experiment hat mit dem Mikroskop zu tun, da durch das Brechen von Licht möglich wird, dass der Lichtstrahl in einer bestimmten Form, durch die einzelnen Materialen und Teile "fließt" und oben bei dem Okular ankommt. Und das Experiment erklärt gut, wie das Brechen von Licht funktioniert.

Material: (Noch nicht fertig!!!!!!!)

Durch die besondere Form der Zersträungslinse (Konkarvlinse)

Sammellinse (Konvexlinse)

Bündeln von Licht

Material: Ein Netzgerät ein Lichtkasten eine Glaslinse (Konvexlinse) zwei Kabel

Aufbau: Zuerst wird das Netzgerät an die Steckdose angeschlossen und die Lampe und das Netzgerät werden mit Kabeln verbunden, die jeweils an den zwölf Volt Steckern angeschlossen sind. Dann schiebt man die Glaslinse in den kleinen Schlitz, am Anfang des Lichtkastens.

Beobachtung: Ohne die Linse verläuft das Licht nicht grade, sondern wird immer breiter. Doch wenn man die Linse einfügt, wird der Lichtstrahl grade, weil die Konvexlinse das Licht bündelt.

Auswertung:

Strahlengänge

Was gibt es für Strahlengänge?

Es gibt den Parallelstrahl, der vor der Linse parallel zur optischen Achse, dann durch den oberen Teil der Linse und zum Schluss durch den Brennpunkt verläuft.

Dann gibt es noch den Brennpunktstrahl, der vor der Linse durch den Brennpunkt, dann durch den unteren Teil der Linse und dann parallel zur optischen Achse verläuft. Also quasi genau anders herum als der Parallelstrahl.

Zu letzt noch der Mittelpunktstrahl, der genau durch den Mittelpunkt der Linse verläuft

Bildkonstruktion und Abbildung zur Linse

http://wikis.zum.de/kas/Datei:Linsengleichung_bam.jpg

Dies ⬆️ ist die zeichnerische Darstellung der Strahlengänge.

Die Linsengleichung, auch Abbildungsgleichung genannt, gibt bei einer optischen Abbildung mit einer Linse den Zusammenhang zwischen Gegenstands-, Bild-, und Brennweite an.

Die Linsengleichung, ist abhängig von der Wölbung der Linse. Je dünner, desto größer das reelle Bild. Je größer die Linse, desto kleiner das durch die Linse erzeugte Bild. Die Rechnung dazu lautet:

$\frac{1}{b}+\frac{1}{g}=\frac{1}{f}$

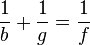
g = Gegenstandsweite b = Bildweite G = Gegenstand B = Bildgröße f = Brennweite

Wenn man g ausrechnen möchte, muss man 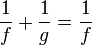$\frac{1}{f}+\frac{1}{g}=\frac{1}{f}$

rechnen.

Wenn man b ausrechnen möchte, muss man 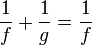$\frac{1}{f}+\frac{1}{g}=\frac{1}{f}$ rechnen.

Außerdem spielt noch die Entfernung des Gegenstandes eine Rolle. Je näher der Gegenstand an der Linse steht, desto größer das reelle Bild. Jeweiter entfernt, desto kleiner das Bild.