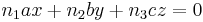Darstellung von Geraden und Ebenen: Unterschied zwischen den Versionen
(→Ebenen) |
(Kategorie:Analytische Geometrie) |
||
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
=== Ebenen === | === Ebenen === | ||
| + | |||
| + | |||
| + | ==== Parameterform: ==== | ||
Eine Ebene wird durch zwei linear unabhängige Richtungsvektoren aufgespannt. | Eine Ebene wird durch zwei linear unabhängige Richtungsvektoren aufgespannt. | ||
| − | Die Parametergleichung für eine Ebene ist | + | Die Parametergleichung für eine Ebene ist: |
<math>E: \vec x=\vec p+r*\vec u+s* \vec v </math> <math>(r, s \in \mathbb{R})</math> | <math>E: \vec x=\vec p+r*\vec u+s* \vec v </math> <math>(r, s \in \mathbb{R})</math> | ||
| + | |||
| + | |||
| + | ==== Normalenform: ==== | ||
| + | |||
| + | <math>[\vec n(\vec x - SV)]= 0</math> | ||
| + | |||
| + | Bei drei gegebenen Vektoren <math>\vec a</math> <math>\vec b</math> <math>\vec c</math> bildet man das Kreuzprodukt aus <math> \vec n =\overrightarrow {ac} \times \overrightarrow {ab}</math><br />. | ||
| + | Der Stützvektor ist <math>\vec a</math>. | ||
| + | |||
| + | ==== Koordinatenform: ==== | ||
| + | |||
| + | <math>\! E: ax+by+cz=d</math> | ||
| + | |||
| + | <br /><br /> | ||
=== Formumformungen === | === Formumformungen === | ||
| + | |||
==== Parameterform in Koordinatenform ==== | ==== Parameterform in Koordinatenform ==== | ||
| + | |||
<math>E: \vec x=\vec p+r*\vec u+s* \vec v </math> <math>\longrightarrow</math> <math>\! E: ax+by+cz=d</math> | <math>E: \vec x=\vec p+r*\vec u+s* \vec v </math> <math>\longrightarrow</math> <math>\! E: ax+by+cz=d</math> | ||
| Zeile 32: | Zeile 51: | ||
<math>\begin{pmatrix} x \\ y \\ z \end{pmatrix}= \vec p+r*\vec u+s* \vec v</math> | <math>\begin{pmatrix} x \\ y \\ z \end{pmatrix}= \vec p+r*\vec u+s* \vec v</math> | ||
| − | Als Gleichungssystem lösen. | + | Als lineares Gleichungssystem lösen. |
| − | + | ||
====Parameterform in Normalenform ==== | ====Parameterform in Normalenform ==== | ||
| − | |||
| + | <math>E: \vec x=\vec p+r*\vec u+s* \vec v </math> <math>\longrightarrow</math> <math>[\vec n(\vec x - SV)]</math> | ||
1) Normalenvektor finden durch <math>\vec n =\vec u \times \vec v</math><br /> | 1) Normalenvektor finden durch <math>\vec n =\vec u \times \vec v</math><br /> | ||
| Zeile 50: | Zeile 68: | ||
Bei 3 Spurpunkten: Parametergleichung aus 3 Punkten. Man wähl einen Stützvektor und zwei Richtungsvektoren.<br /> | Bei 3 Spurpunkten: Parametergleichung aus 3 Punkten. Man wähl einen Stützvektor und zwei Richtungsvektoren.<br /> | ||
Bei 2 Spurpunkten S<sub>x</sub>,s<sub>y</sub>: Ebene liegt parallel zur <math>z</math> damit ist der Richtungvektor <math>\begin{pmatrix} 0 \\ 0\\ 1 \end{pmatrix}</math><br /> | Bei 2 Spurpunkten S<sub>x</sub>,s<sub>y</sub>: Ebene liegt parallel zur <math>z</math> damit ist der Richtungvektor <math>\begin{pmatrix} 0 \\ 0\\ 1 \end{pmatrix}</math><br /> | ||
| − | |||
====Koordinatenform in Normalenform==== | ====Koordinatenform in Normalenform==== | ||
| − | |||
| + | <math>\vec n</math>bestimmen durch Koeffizienten der Koordinatenform <Math>\! E: ax+by+cz=d</math> also <math>\vec n=\begin{pmatrix} a \\ b\\ c \end{pmatrix}</math> | ||
Als Stützvektor wählt man einen Spurpunkt. | Als Stützvektor wählt man einen Spurpunkt. | ||
Zielgleichung: <math>[\begin{pmatrix} a \\ b\\ c \end{pmatrix}(\vec x - Spurpunkt)]</math> | Zielgleichung: <math>[\begin{pmatrix} a \\ b\\ c \end{pmatrix}(\vec x - Spurpunkt)]</math> | ||
| − | |||
==== Normalenform in Koordinatenform ==== | ==== Normalenform in Koordinatenform ==== | ||
| + | <br /> | ||
Ausmultiplizieren des Skalarprodukts. | Ausmultiplizieren des Skalarprodukts. | ||
Zielgleichung: <math>\!n_1ax+n_2by+n_3cz=0</math> | Zielgleichung: <math>\!n_1ax+n_2by+n_3cz=0</math> | ||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Analytische Geometrie]] | ||
Aktuelle Version vom 27. Dezember 2010, 11:49 Uhr
Inhaltsverzeichnis |
Geraden
Eine Gerade ist durch zwei Punkte definiert.
In der vektoriellen Darstellung ist eine Gerade durch einen Stützvektor 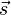 und einen Richtungsvektor
und einen Richtungsvektor 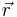 beschrieben.
beschrieben.
Die Geradengleichung in Parameterform ist also:
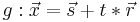
Bei zwei gegebenen Punkten A und B ist z.B. 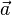 der Stützvektor und
der Stützvektor und 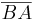 der Richtungsvektor.
der Richtungsvektor.
Ebenen
Parameterform:
Eine Ebene wird durch zwei linear unabhängige Richtungsvektoren aufgespannt.
Die Parametergleichung für eine Ebene ist:
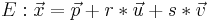
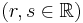
Normalenform:
![[\vec n(\vec x - SV)]= 0](/images/math/4/4/3/4435afb0b61b5e8ad4a9d3265efe5abd.png)
Bei drei gegebenen Vektoren 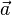
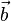
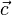 bildet man das Kreuzprodukt aus
bildet man das Kreuzprodukt aus 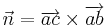
.
Der Stützvektor ist 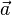 .
.
Koordinatenform:
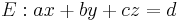
Formumformungen
Parameterform in Koordinatenform
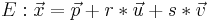
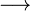
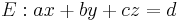
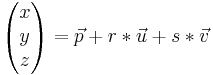
Als lineares Gleichungssystem lösen.
Parameterform in Normalenform
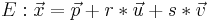
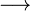
![[\vec n(\vec x - SV)]](/images/math/9/f/8/9f85ae46d2cfae3704305609e34358d4.png)
1) Normalenvektor finden durch 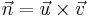
2) Der Stützvektor bleibt gleich
Zielgleichung: ![[\vec u \times \vec v(\vec x - \vec p)]](/images/math/9/5/0/9507c4edf43a94817ff34bb89acee04f.png)
Koordinatenform in Parameterform
Bei 3 Spurpunkten: Parametergleichung aus 3 Punkten. Man wähl einen Stützvektor und zwei Richtungsvektoren.
Bei 2 Spurpunkten Sx,sy: Ebene liegt parallel zur 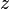 damit ist der Richtungvektor
damit ist der Richtungvektor 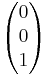
Koordinatenform in Normalenform
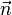 bestimmen durch Koeffizienten der Koordinatenform
bestimmen durch Koeffizienten der Koordinatenform 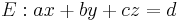 also
also 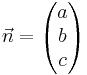 Als Stützvektor wählt man einen Spurpunkt.
Als Stützvektor wählt man einen Spurpunkt.
Zielgleichung: ![[\begin{pmatrix} a \\ b\\ c \end{pmatrix}(\vec x - Spurpunkt)]](/images/math/d/c/3/dc3fd53b5009a700c3641b4091bbb80e.png)
Normalenform in Koordinatenform
Ausmultiplizieren des Skalarprodukts.
Zielgleichung: