Der Artikel der 9b: Unterschied zwischen den Versionen
| Zeile 91: | Zeile 91: | ||
[[Datei:Image123koordinatensystem.jpg|Meisner|400px]] | [[Datei:Image123koordinatensystem.jpg|Meisner|400px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''WEITERES EXPERIMENT (neu)''' '''=Ohmsche Gesetz''' | ||
| + | |||
| + | '''Durch den vorherigen Versuch, kamen wir zu diesen Überlegungen.''' | ||
| + | |||
| + | Ein proportionaler Zusammenhang bedeutet, dass wenn sich eine Größe durch einen Faktor verändert, verändert sich auch die andere Größe um denselben Faktor. | ||
| + | Das bedeutet also, dass auch ein Zusammenhang zwischen '''U''' und '''I''' besteht. (Wenn sich dann also '''I''' ändert, dann auch '''U''' ). | ||
| + | |||
| + | Erster Schritt: Wir haben einen Stromkreis aufgebaut (nur mit einer Lampe). Dann haben wir die Stromstärke (an der Quelle) und die elektrische Leistung (im Stromkreis) gemessen. | ||
| + | |||
| + | I = elektrische Stromstärke | ||
| + | |||
| + | U = elektrische Spannung | ||
| + | |||
| + | Schließlich haben wir versucht einen funktionalen Zusammenhang zwischen Widerstand, elektrischer Stromstärke und Spannung herauszufinden , anhand einer WERTETABELLE ( http://wikis.zum.de/kas/images/f/f9/Bild_Image.jpg ) und einer ZEICHNUNG VON EINEM GRAPHEN. | ||
| + | |||
| + | [[Datei:Imagel.jpg|400px]] | ||
| + | |||
| + | [[Datei:Imagem.jpg|400px]] | ||
| + | |||
| + | [[Datei:Imageklm.jpg|400px]] | ||
| + | |||
| + | |||
| + | Wir haben für die Ergebnisse mehrere Lampen benutzt: ,,Normale Lampe", ,,47er Widerstand", ,,100er Widerstand" | ||
| + | Dadurch haben wir verschiedene Ergebnisse herausgefunden. (Siehe Links unten) | ||
| + | |||
| + | Wir kamen zum Entschluss, dass alle Graphen durch den '''0-Punkt''' gehen, deshalb ist es eine '''Proportionale Funktion'''. | ||
| + | |||
| + | Allgemeine Formel für die Proportionale Funktion: <math> f(x) = mx </math> | ||
| + | |||
| + | <math> m </math> steht hier für die Steigung innerhalb der einzelnen Punkte | ||
| + | |||
| + | |||
| + | |||
| + | Das <math> m </math> findet man heraus indem man die Formel: | ||
| + | |||
| + | <math> m=\frac{I_{2}-I_{1}}{U_{2}-U_{1}}</math> | ||
| + | |||
| + | benutzt. | ||
| + | |||
| + | |||
| + | Setzt man nun für <math> m </math> = '''0.02''' ein, entsteht die Formel: | ||
| + | |||
| + | |||
| + | <math> m=\frac{0,02A}{1V} *x</math> <-gilt für die 47-Lampe | ||
| + | |||
| + | Kehrwert: <math> m=50 </math> | ||
| + | |||
| + | Da der Kehrwert 50 beträgt, besteht ein Zusammenhang zwischen dem Widerstand und der gemessenen Größe ( <math> m=\frac{0,02A}{1V} *x</math> ) | ||
| + | |||
| + | SO KANN MAN DEN GRAPH WEITERFÜHREN (man kann weitere Zahlen einsetzen und dies anhand einer Rechnung herausfinden) | ||
| + | |||
| + | Wenn man den Kehrwert anwendet kommt man zur Formel des Ohm-Zeichen. | ||
| + | |||
| + | |||
| + | Die größe hier heißt ,,elektrischer Wiederstand'' | ||
| + | |||
| + | Formelzeichen = <math> R </math> Ω <math> = \frac{V}{A} </math> | ||
| + | |||
| + | Ω = Ohm-Zeichen | ||
| + | |||
| + | |||
| + | Zusammenhang zwischen U,I,R: <math> R </math> <math>=\frac{U}{I} </math> | ||
| + | |||
| + | |||
| + | Dies ist das '''Ohmsche Gesetz''' | ||
Version vom 18. Februar 2015, 12:08 Uhr
Energietransport
In diesem Wikiartikel beschäftigte sich die Gruppe vor uns mit der Frage 'Was ist Strom?' und wir beschäftigen uns nun mit den Fragen 'Was sind elektrische Größen?' und wie man einen elektrischen Stromkreis mit einen Wasserkreislauf vergleichen kann.
Elektrische Größen
Vereinfacht kann man sagen, dass phy.Größen in verschiedenen Einheiten gemessen werden und sie verschiedene Formelzeichen haben.
'Die elektrische Spannung (U) wird in (V) gemessen und gibt an wie viel Energie eine Ladung hat(U V=J:C).
'Die elektrische Leistung (P) wird in (W) gemessen und gibt Energie pro Zeit an(P W=J:S)
Die elektrische Stromstärke (I) wird in (A) gemessen und beschreibt die Ladung(I A=C:S)
Der Widerstand beschreibt die Leitfähigkeit(V:A=R)
Die Einheiten haben verschiedene Bedeutungen
V=Volt/ W=Watt/ A=Ampere/ J=Energie/ S=Sekunde/ C=Coulomb/
Aus all diesen Werten kann man sich die oberen Werte erschliessen.(Wir haben dies in Experimenten erschlossen)
Wie kann man einen elektrischen Stromkreis mit einem Wasserkreislauf vergleichen
Einen Wasserkreislauf kann man vereinfacht gut mit einem Stromkreis vergleichen man kann bei einem Wasserkreislauf genau erkennen wie man die Fliessgeschwindigkeit beeinflussen kann in dem man die Strecke verändert
Wenn man ein zB ein Wasserrohr an einer Stelle schmaler macht, dann fließt das Wasser langsamer und staut sich. Wenn man ein Wasserohr an einer Stelle breiter macht,desto mehr Wasser kann vorbei fließen und die Fließgeschwindigkeit steigt.
Man kann die Spannung auf ein Wasserteilchen betrachten in dem man schaut wie viel Ladung es hat.
Ebenfalls die Leistung kann man auf einen Wasserkreislauf übertragen,indem man schaut wie viel Energie pro Zeit ,also Wasser pro Zeit an einer bestimmten Stelle vorbeifliesst.
Die Stromstärke beschreibt den Druck und die Ladung des Wassers.
Dieses Phänomen kann man mit Hinsicht auf Kabel auf einen Stromkreis übertragen.
Der Wiederstand ist vom Rohr ,Material,dicke abhänig und dies kann man ebenfalls auf Wasser übertragen.
Die nächste Gruppe wird sich auf Dräthe und deren Leitfähigkeit beziehen.
Das Draht Experiment
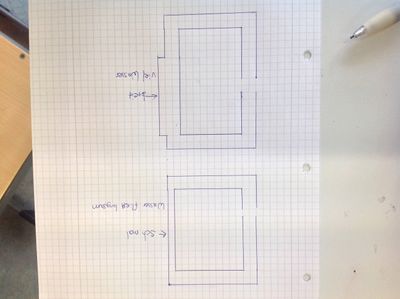
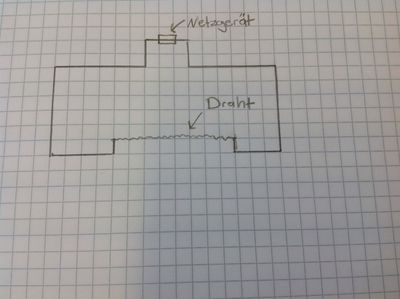
Jetzt haben wir versucht eine Gleichmäßigkeit zwischen den größen zu finden und zu gucken ob die Länge eines Drahtes( lang, mittel, kurz) etwas mit den verschiedenen größen zu tun hat. Wir haben dann einen Stromkreis aufgebaut und die verschiedene Drähte eingespannt. Beim längsten war die elektrische Stromstärke am höchsten, beim Kürzesten am wenigsten. Das heißt, dass längere Drähte mehr elektrische stromstärke brauchen. Ein weiterer grund ist, dass der Draht viel Dünner ist, als der rest der Kabel im Stromkreis. Der Strom wird also von einem normalen Draht in ein viel dünneren Draht gequetscht und braucht mehr stromstärke um durch die Verengung zukommen.
Aus den zwei Werten haben wir dann (R) also den Wiederstand berechnet
| Länge | U | I | R |
|---|---|---|---|
| 16,5cm | 2 | 2,26 | 0,88 |
| 3,82 | 3,65 | 1,46 | |
| 5,81 | 5,6 | 1,37 | |
| 46,5cm | 2 | 0,83 | 2,40 |
| 3,81 | 1,53 | 2,4 | |
| 5,80 | 2,28 | 2,5 | |
| 115cm | 2 | 0,35 | 5,55 |
| 3,54 | 0,79 | 4,8 | |
| 5,82 | 1,19 | 4,8 |
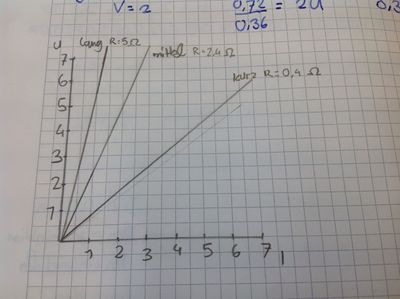
Wir haben für jeden Graphen einen Funktionsterm gefunden:
Lang: f(x)=5x
Mittel: f(x)=2x
Kurz: f(x)=0,4x
WEITERES EXPERIMENT (neu) =Ohmsche Gesetz
Durch den vorherigen Versuch, kamen wir zu diesen Überlegungen.
Ein proportionaler Zusammenhang bedeutet, dass wenn sich eine Größe durch einen Faktor verändert, verändert sich auch die andere Größe um denselben Faktor. Das bedeutet also, dass auch ein Zusammenhang zwischen U und I besteht. (Wenn sich dann also I ändert, dann auch U ).
Erster Schritt: Wir haben einen Stromkreis aufgebaut (nur mit einer Lampe). Dann haben wir die Stromstärke (an der Quelle) und die elektrische Leistung (im Stromkreis) gemessen.
I = elektrische Stromstärke
U = elektrische Spannung
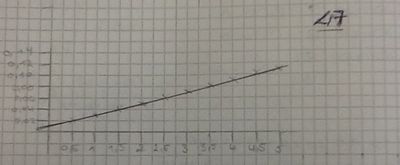
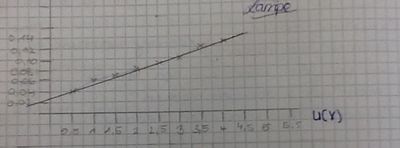
Schließlich haben wir versucht einen funktionalen Zusammenhang zwischen Widerstand, elektrischer Stromstärke und Spannung herauszufinden , anhand einer WERTETABELLE ( http://wikis.zum.de/kas/images/f/f9/Bild_Image.jpg ) und einer ZEICHNUNG VON EINEM GRAPHEN.
Wir haben für die Ergebnisse mehrere Lampen benutzt: ,,Normale Lampe", ,,47er Widerstand", ,,100er Widerstand"
Dadurch haben wir verschiedene Ergebnisse herausgefunden. (Siehe Links unten)
Wir kamen zum Entschluss, dass alle Graphen durch den 0-Punkt gehen, deshalb ist es eine Proportionale Funktion.
Allgemeine Formel für die Proportionale Funktion: 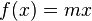
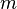 steht hier für die Steigung innerhalb der einzelnen Punkte
steht hier für die Steigung innerhalb der einzelnen Punkte
Das 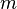 findet man heraus indem man die Formel:
findet man heraus indem man die Formel:
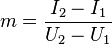
benutzt.
Setzt man nun für 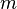 = 0.02 ein, entsteht die Formel:
= 0.02 ein, entsteht die Formel:
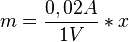 <-gilt für die 47-Lampe
<-gilt für die 47-Lampe
Kehrwert: 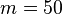
Da der Kehrwert 50 beträgt, besteht ein Zusammenhang zwischen dem Widerstand und der gemessenen Größe ( 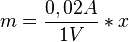 )
)
SO KANN MAN DEN GRAPH WEITERFÜHREN (man kann weitere Zahlen einsetzen und dies anhand einer Rechnung herausfinden)
Wenn man den Kehrwert anwendet kommt man zur Formel des Ohm-Zeichen.
Die größe hier heißt ,,elektrischer Wiederstand
Formelzeichen = 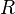 Ω
Ω 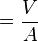
Ω = Ohm-Zeichen
Zusammenhang zwischen U,I,R: 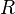
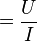
Dies ist das Ohmsche Gesetz
5.Experiment: Unterschiedliche Lampen und Wiederstände/Neue Grösse
Wir haben Stromkreise mit unterschiedlichen Lampen ( Wiederständen ) aufgebaut und bei allen Lampen jeweils die Stromstärke bei 1, 2, 3... und so weiter Volt gemessen:
Ergebnisse Lampe:
| Spannung | Stromstärke |
|---|---|
| 1 Volt | 0,08 Ampere |
| 2 Volt | 0,1 Ampere |
| 3 Volt | 0,12 Ampere |
| 4 Volt | 0,14 Ampere |
| 5 Volt | 0,16 Ampere |
| 6 Volt | 0,18 Ampere |
| 7 Volt | 0,2 Ampere |
| 8 Volt | 0,22 Ampere |
| 9 Volt | 0,24 Ampere |
| 10 Volt | 0,26 Ampere |
Ergebnisse 47er Wiederstand:
| Spannung | Stromstärke |
|---|---|
| 1 Volt | 0,02 Ampere |
| 2 Volt | 0,04 Ampere |
| 3 Volt | 0,06 Ampere |
| 4 Volt | 0,08 Ampere |
| 5 Volt | 0,1 Ampere |
| 6 Volt | 0,12 Ampere |
| 7 Volt | 0,14 Ampere |
| 8 Volt | 0,16 Ampere |
| 9 Volt | 0,18 Ampere |
| 10 Volt | 0,2 Ampere |
Ergebnisse 150er Wiederstand:
| Spannung | Stromstärke |
|---|---|
| 1 Volt | 0,01 Ampere |
| 2 Volt | 0,02 Ampere |
| 3 Volt | 0,03 Ampere |
| 4 Volt | 0,04 Ampere |
| 5 Volt | 0,05 Ampere |
| 6 Volt | 0,06 Ampere |
| 7 Volt | 0,07 Ampere |
| 8 Volt | 0,08 Ampere |
| 9 Volt | 0,09 Ampere |
| 10 Volt | 0,1 Ampere |
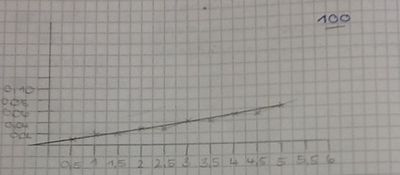
Diese Ergebnisse haben wir dann als Graphen in Koordinatensysteme gezeichnet, um daraus die Funktionen heraus zu kriegen:
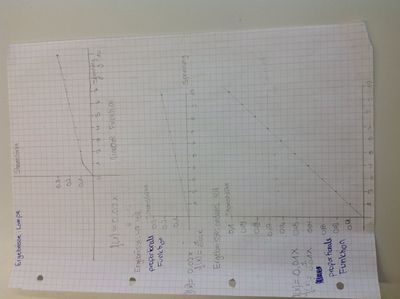
F(x) = m•x, d. h. Es ist eine proportionale Funktion
Beispiel: Wir haben einen Graphen mit der Steigung f(x)=0,02x m=0,02Ampere:1Volt=0,02•(Ampere:Volt) I(x)=0,02•((Ampere:Volt)•x) Wenn wir jetzt unser Netzgerät auf z.B. 5 V stellen würden, dann müsste in Strom von: I(5)=0,02•(Ampere•5)=0,1 Ampere Der proportionale Faktor wird als neue physikalische Grösse eingeführt. Die Grösse heisst hier elektrischer Wiederstand. Formelzeichen: R [ Ω ] = [ Volt:Ampere ] Zusammenhang: I, U, R : R= U:I Ohmsches Gesetz
Gruppe 6: Methode: Funktionale Zusammenhänge + physikalische Größen aus einem Experiment ableiten
Wenn zwei Größen funktional zusammenhängend sind, dann verändern sich die Größen immer verhältnismäßig gleich zueinander.
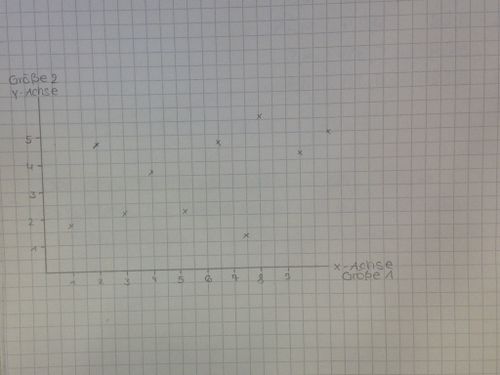
Beispiel A: Addiert man zu Größe 1 den Wert 2, addiert sich zur Größe 2 auch der Wert 2. Dies trifft bei linearen Funktionen zu.
Beispiel B: Verdoppelt man Größe 1, verdoppelt sich auch Größe 2. Dies trifft nur bei proportionalen Funktionen zu.
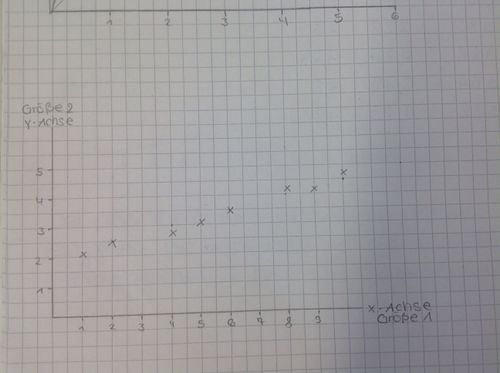
Nicht erkennbar als linearer Graph:
Beispiel für eine lineare Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 2 | 2,5 |
| 4 | 3 |
| 6 | 3,5 |
| 8 | 4 |
| 10 | 4,5 |
Eingezeichnete Punkte einer linearen Funktion:
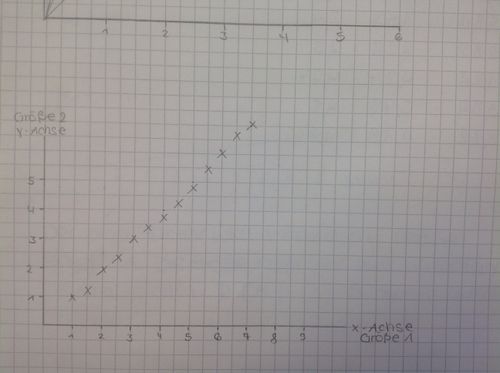
Beispiel für eine proportionale Funktion:
| Größe 1 | Größe 2 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
Eingezeichnete Punkte einer proportionalen Funktion:
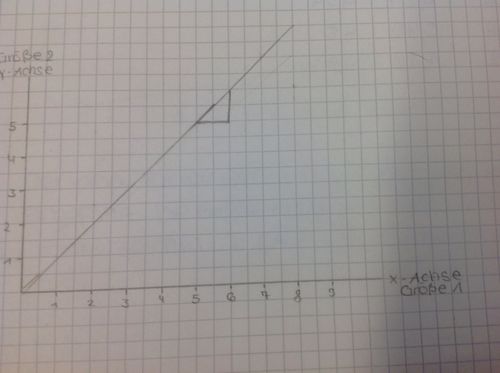
Zunächst wurden von uns zwei physikalische Größen gemessen, wobei wir bewusst eine Größe verändert und die andere gemessen haben, die Messwerte haben wir dann in eine Wertetabelle eingetragen. Die Größen haben wir danach in einem Koordiantensystem jeweils auf der x- und y-Achse eingezeichnet und nun werden Punkte im Koordinatensystem markiert, die den gemessen Werten entsprechen. Dann wird ein Graph in Form einer Gerade gezogen. Falls man von einer proportionalen Funktion ausgeht, zieht man ein Gerade vom Nullpunkt aus, welche möglichst viele Messpunkte überschneidet, wobei sich die Steigung errechnen lässt, wenn man Wert x mit dem entsprechenden Wert y dividiert. Geht man jedoch von einer quadratischen Funktion aus, quadriert man die eine Größe und teilt sie durch die andere Größe, aus welcher sich die Steigung ergibt.
Daraufhin wird das Steigungsdreieck errechnet/abgelesen. Das Steigungsdreieck errechnet man, indem man schaut, um wie viel sich das y verändert, wenn sich x um eins erhöht. Die Steigung beschreibt, um wie viel der y-Wert pro x sich verändert.
Hierbei beträgt die Steigung 1, denn wenn x um 1 erhöht wird erhöht sich auch y um genau 1.
Daraus kann man den Funktionsterm y=mx bilden, wobei m für die Steigung des Graphen steht. Die neu entstandene physikalische Größe kann errechnet werden, indem man x durch y teilt.