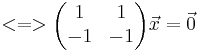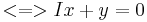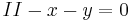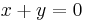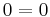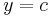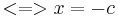Eigenwerte und Eigenvektoren (Fixelemente).: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition)
(typo)
Zeile 1: Zeile 1:
−
'''
 
 
== Definition ==
 
== Definition ==
−
'''
 
−
Ein Eigenvektor einer Abbildung  ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur gestreckt, und man bezeicnet den Streckungsfaktor als Eigenwert der Abbildung.
 
  
−
Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssydtem eindeutig lösbar ist oder nicht. In vielen Anwendungen beschreibenEigenwerte auch physikalische Eigenschaften eines mathematischen Modells.[www.uni-leipzig.de/stksachs/lehrbuecher/.../eigenwerte.pdf ], 14.12.2009
+
Ein Eigenvektor einer Abbildung  ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur gestreckt, und man bezeichnet den Streckungsfaktor als Eigenwert der Abbildung.
 +
 
 +
Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssystem eindeutig lösbar ist oder nicht. In vielen Anwendungen beschreiben Eigenwerte auch physikalische Eigenschaften eines mathematischen Modells.[www.uni-leipzig.de/stksachs/lehrbuecher/.../eigenwerte.pdf ], 14.12.2009
  
 
== Bestimmung von Eigenwerten ==
 
== Bestimmung von Eigenwerten ==
Zeile 12: Zeile 11:
 
\end{pmatrix}</math>.
 
\end{pmatrix}</math>.
  
−
Aufstellen der '''''charakteristischen Gleichung:''''' <br />
+
Aufstellen der '''''charakteristischen Gleichung:'''''  
  
−
                      <math>det(A-\lambda A)=0<=>(a-\lambda)(d-\lambda)-bc=0\!\,</math>
+
<math>det(A-\lambda A)=0<=>(a-\lambda)(d-\lambda)-bc=0\!\,</math>
  
 
Die Lösungen '''<math>\lambda</math><sub>1</sub>/<math>\lambda</math><sub>2</sub>''' dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.
 
Die Lösungen '''<math>\lambda</math><sub>1</sub>/<math>\lambda</math><sub>2</sub>''' dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.
  
 
== Bestimmung von Eigenvektoren ==
 
== Bestimmung von Eigenvektoren ==
−
Die Eigenvektoren erhält man, indem man das LGS <math>\begin{pmatrix}
+
Die Eigenvektoren erhält man, indem man das LGS <math>\begin{pmatrix}
 
a-\lambda & c \\
 
a-\lambda & c \\
 
b & d-\lambda
 
b & d-\lambda
Zeile 58: Zeile 57:
  
 
'''<math>=>\vec x = c{-1 \choose 1}\!\,</math>'''
 
'''<math>=>\vec x = c{-1 \choose 1}\!\,</math>'''
 +
 +
 +
[[Kategorie:Vektorrechnung]]

Version vom 14. Dezember 2009, 19:29 Uhr

Inhaltsverzeichnis

Definition

Ein Eigenvektor einer Abbildung ist in der linearen Algebra ein vom Nullvektor verschiedener Vektor, dessen Richtung durch die Abbildung nicht verändert wird. Ein Eigenvektor wird also nur gestreckt, und man bezeichnet den Streckungsfaktor als Eigenwert der Abbildung.

Eigenwerte charakterisieren wesentliche Eigenschaften linearer Abbildungen, etwa ob ein entsprechendes lineares Gleichungssystem eindeutig lösbar ist oder nicht. In vielen Anwendungen beschreiben Eigenwerte auch physikalische Eigenschaften eines mathematischen Modells.[www.uni-leipzig.de/stksachs/lehrbuecher/.../eigenwerte.pdf ], 14.12.2009

Bestimmung von Eigenwerten

Gegeben ist die Abbildungsmatrix A=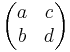\begin{pmatrix} a & c\\ b & d \end{pmatrix}.

Aufstellen der charakteristischen Gleichung:

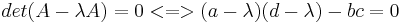
det(A-\lambda A)=0<=>(a-\lambda)(d-\lambda)-bc=0\!\,

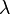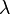Die Lösungen \lambda1/\lambda2 dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.

Bestimmung von Eigenvektoren

Die Eigenvektoren erhält man, indem man das LGS 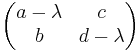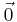\begin{pmatrix} a-\lambda & c \\ b & d-\lambda \end{pmatrix} \vec x=\vec0 löst.

Für den Eigenwert 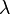\lambda=1 erhält man eine Fixpunktgerade, für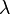 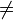\lambda\ne1 eine Fixgerade.

Beispielaufgaben

Bestimmung der Eigenwerte:

Gegeben ist die Matrix 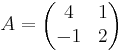A=\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix}\!\,

Aufstellen der charakteristischen Gleichung: 

                                           (4-\lambda)(2-\lambda)+1=0\!\,
                                     <=>\lambda^2-6\lambda+8+1=0\!\,
                                     <=>\lambda^2-6\lambda+9=0\!\,
                                     <=>\lambda_{1,2}=3\pm\sqrt{9-9}\!\,
                                     <=>\lambda_{1,2}=3\!\,

=>d.h. nur ein Eigenwert

Bestimmung des Eigenvektors: 

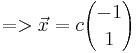
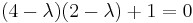
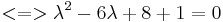
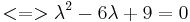
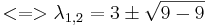
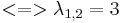
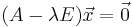
                                          (A-\lambda E)\vec x=\vec 0\!\,
                                    <=>\left[\begin{pmatrix} 4 & 1 \\ -1 & 2 \end{pmatrix} -\begin{pmatrix} 3 & 0 \\ 0 & 3\end{pmatrix}\right]\vec x=\vec 0\!\, 
                                    <=>\begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix}\vec x=\vec 0\!\,

                                    <=>I x+y=0\!\,
                                             II -x-y=0\!\,

                                          x+y=0\!\,
                                          0=0\!\,

                                          y=c\!\,
                                    <=> x=-c\!\,

=>\vec x = c{-1 \choose 1}\!\,

Von „http://kas.zum.de/index.php?title=Eigenwerte_und_Eigenvektoren_(Fixelemente).&oldid=1017“