G9: Strecken und Verschieben der Normalparabel: f(x)=a(x-d)²+e: Unterschied zwischen den Versionen
Aus KAS-Wiki
(→Strecken und Stauchen der Parabel) |
|||
| (17 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | == Strecken und Verschieben der Normalparabel: f(x)=a(x-d)²+e == | |
| − | # Mit dieser Formel ist es möglich, sowohl die Normalparabel entlang der x- bzw. der y-Achse zu verschieben,als auch zu strecken | + | # Mit dieser Formel ist es möglich, sowohl die Normalparabel entlang der x- bzw. der y-Achse zu verschieben,als auch zu strecken oder zu stauchen. |
| − | + | ||
| − | + | === Verschiebung entlang der y-Achse === | |
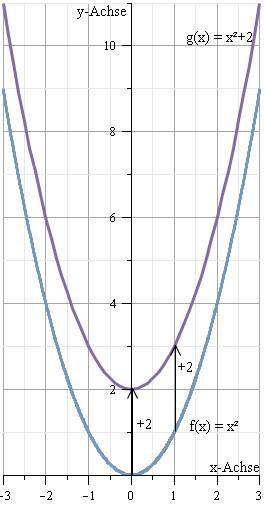
| + | Das "e" steht für die Verschiebung der Normalparabel entlang der y-Achse, ist dieser Wert positiv, so verschiebt sie sich nach oben, ist er negativ, so verschiebt sie sich nach unten. | ||
| + | |||
| + | f(x)=x²+e | ||
[[Bild:verschieben_der_normalparabel_in_y_richtung_clip_image002.jpg]] | [[Bild:verschieben_der_normalparabel_in_y_richtung_clip_image002.jpg]] | ||
| − | + | *Die Symmetrieachse ist immer "y". | |
| − | + | *f(x)=x²+2 | |
| − | Ohne diese Formel auszurechnen, kann man den Scheitelpunkt ablesen. Bei dieser Formel ist der x-Wert immer 0 und der y-Wert entspricht e. In diesem Fall, 2. S(0/2) | + | *Ohne diese Formel auszurechnen, kann man den Scheitelpunkt ablesen. Bei dieser Formel ist der x-Wert immer 0 und der y-Wert entspricht e. In diesem Fall, 2. S(0/2) |
| − | + | === Verschiebung entlang der x-Achse === | |
| − | f(x)=(x-d)² | + | |
| + | Das "-d" steht für die Verschiebung der Normalparabel entlang der x-Achse, ist dieser Wert negativ, verschiebt sie sich nach rechts, ist dieser Wert positiv, verschiebt sie sich nach links. | ||
| + | |||
| + | *f(x)=(x-d)² | ||
[[Bild:Parabelnd.jpg]] | [[Bild:Parabelnd.jpg]] | ||
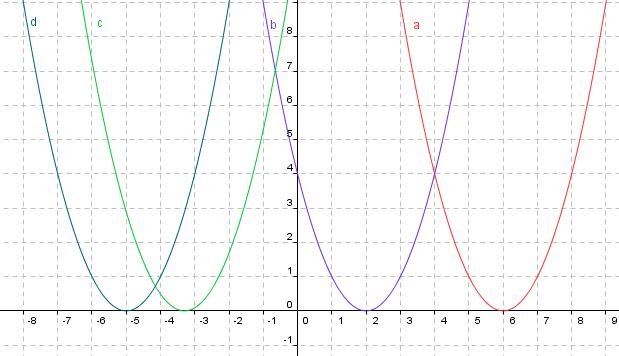
| − | Graph "a" entspricht der Gleichung: f(x)=(x-6)² | + | *Graph "a" entspricht der Gleichung: f(x)=(x-6)² |
| − | Graph "b" entspricht der Gleichung: f(x)=(x-2)² | + | *Graph "b" entspricht der Gleichung: f(x)=(x-2)² |
| − | Graph "c" entspricht der Gleichung: f(x)=(x+3.5)² | + | *Graph "c" entspricht der Gleichung: f(x)=(x+3.5)² |
| − | Graph "d" entspricht der Gleichung: f(x)=(x+5)² | + | *Graph "d" entspricht der Gleichung: f(x)=(x+5)² |
| − | Ist der Wert "d" positiv (Bsp. +3.5), liegt der Graph im negativen Bereich. | + | *Ist der Wert "d" positiv (Bsp. +3.5), liegt der Graph im negativen Bereich. |
| − | Ist der Wert "d" negativ (Bsp. -2), liegt der Graph im positiven Bereich. | + | *Ist der Wert "d" negativ (Bsp. -2), liegt der Graph im positiven Bereich. |
| − | "-d" enstricht der Symmetrieachse. Zu beachten ist hierbei, dass man immer den Wert "d" gebraucht. (Bsp: f(x)=(x-2)², die Symmetrieachse läge in diesem Fall bei eins. | + | *"-d" enstricht der Symmetrieachse. Zu beachten ist hierbei, dass man immer den Wert "d" gebraucht. (Bsp: f(x)=(x-2)², die Symmetrieachse läge in diesem Fall bei eins. |
| − | Das "a" in der Gleichung vor der | + | === Strecken und Stauchen der Parabel === |
| − | + | ||
| − | + | Das "a" in der Gleichung vor der Klammer steht für die Sreckung bzw. Stauchung und Öffnung der Normalparabel | |
| − | + | *Gilt a>1, so wird die Parabel gestreckt. | |
| − | Ist der Wert positiv (+5), ist die Parabel nach | + | *Gilt 0<a<1, so wird die Parabel gestaucht. |
| + | *Ist der Wert negativ (z.B. a=-5), ist die Parabel nach unten geöffnet. | ||
| + | *Ist der Wert positiv (z.B. a=+5), ist die Parabel nach oben geöffnet. | ||
f(x)=ax² | f(x)=ax² | ||
[[Bild:strecken_stauchen_spiegeln_einer_quadratischen_funktion_clip_image002.jpg]] | [[Bild:strecken_stauchen_spiegeln_einer_quadratischen_funktion_clip_image002.jpg]] | ||
| − | |||
| − | |||
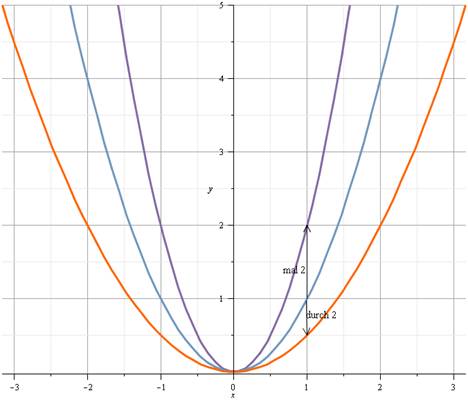
| − | + | *In dieser Graphik ist der blaue Graph, die Normalparabel. Der Rote ist eine gestauchte, der Violette eine gestreckte Parabel. | |
| + | |||
| + | Wenn man alle diese Möglichkeiten verbindet, erhält man die Formel: f(x)=a(x-d)²+e | ||
Diese Parabel ermöglicht uns das verschieben sowohl auf der x- als auch auf der y-Achse. Zusätzlich verliert sie die Normalform, durch das Strecken/Stauchen der Parabel. | Diese Parabel ermöglicht uns das verschieben sowohl auf der x- als auch auf der y-Achse. Zusätzlich verliert sie die Normalform, durch das Strecken/Stauchen der Parabel. | ||
| + | |||
| + | === Übungen === | ||
| + | |||
| + | *Zu Verschiebungen, sowohl auf der x- als auch auf der y-Achse | ||
| + | **http://www.tiburski.de/cybernautenshop/virtuelle_schule/dfu/quadratische_funktionen/index2.html | ||
| + | **http://www.dynama.de/hotmath/9/normparab/normparab.htm | ||
| + | **http://www.mathe-trainer.de/Klasse9/Quadratische_Funktionen/Block6/Aufgaben.htm | ||
| + | *Zum Strecken und Stauchen der Parabel | ||
| + | **http://www.tiburski.de/cybernautenshop/virtuelle_schule/dfu/quadratische_funktionen/index.html | ||
| + | |||
| + | |||
| + | [[Kategorie:Quadratische Funktionen]] | ||
Aktuelle Version vom 24. März 2013, 14:17 Uhr
Inhaltsverzeichnis |
Strecken und Verschieben der Normalparabel: f(x)=a(x-d)²+e
- Mit dieser Formel ist es möglich, sowohl die Normalparabel entlang der x- bzw. der y-Achse zu verschieben,als auch zu strecken oder zu stauchen.
Verschiebung entlang der y-Achse
Das "e" steht für die Verschiebung der Normalparabel entlang der y-Achse, ist dieser Wert positiv, so verschiebt sie sich nach oben, ist er negativ, so verschiebt sie sich nach unten.
- Die Symmetrieachse ist immer "y".
- f(x)=x²+2
- Ohne diese Formel auszurechnen, kann man den Scheitelpunkt ablesen. Bei dieser Formel ist der x-Wert immer 0 und der y-Wert entspricht e. In diesem Fall, 2. S(0/2)
Verschiebung entlang der x-Achse
Das "-d" steht für die Verschiebung der Normalparabel entlang der x-Achse, ist dieser Wert negativ, verschiebt sie sich nach rechts, ist dieser Wert positiv, verschiebt sie sich nach links.
- f(x)=(x-d)²
- Graph "a" entspricht der Gleichung: f(x)=(x-6)²
- Graph "b" entspricht der Gleichung: f(x)=(x-2)²
- Graph "c" entspricht der Gleichung: f(x)=(x+3.5)²
- Graph "d" entspricht der Gleichung: f(x)=(x+5)²
- Ist der Wert "d" positiv (Bsp. +3.5), liegt der Graph im negativen Bereich.
- Ist der Wert "d" negativ (Bsp. -2), liegt der Graph im positiven Bereich.
- "-d" enstricht der Symmetrieachse. Zu beachten ist hierbei, dass man immer den Wert "d" gebraucht. (Bsp: f(x)=(x-2)², die Symmetrieachse läge in diesem Fall bei eins.
Strecken und Stauchen der Parabel
Das "a" in der Gleichung vor der Klammer steht für die Sreckung bzw. Stauchung und Öffnung der Normalparabel
- Gilt a>1, so wird die Parabel gestreckt.
- Gilt 0<a<1, so wird die Parabel gestaucht.
- Ist der Wert negativ (z.B. a=-5), ist die Parabel nach unten geöffnet.
- Ist der Wert positiv (z.B. a=+5), ist die Parabel nach oben geöffnet.
- In dieser Graphik ist der blaue Graph, die Normalparabel. Der Rote ist eine gestauchte, der Violette eine gestreckte Parabel.
Wenn man alle diese Möglichkeiten verbindet, erhält man die Formel: f(x)=a(x-d)²+e Diese Parabel ermöglicht uns das verschieben sowohl auf der x- als auch auf der y-Achse. Zusätzlich verliert sie die Normalform, durch das Strecken/Stauchen der Parabel.
Übungen
- Zu Verschiebungen, sowohl auf der x- als auch auf der y-Achse
- Zum Strecken und Stauchen der Parabel