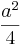Ganzrationale Funktionen: Unterschied zwischen den Versionen
Eva P. (Diskussion | Beiträge) |
|||
| Zeile 2: | Zeile 2: | ||
| + | |||
| + | <math>a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0</math> = Polynom | ||
| + | |||
| + | <math>a_n, a_8n-1,..., a_1, a_0</math> = Koeffizienten | ||
| + | |||
| + | n = Grad des Polynom | ||
| Zeile 54: | Zeile 60: | ||
| + | |||
| + | |||
| + | '''Verhalten von ganzrationalen Funktionen : ''' | ||
| + | |||
| + | <math>a_nx^n</math> : für <math>a_n > 0</math> gilt | ||
Version vom 3. Dezember 2009, 11:24 Uhr
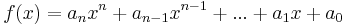
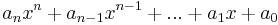= Polynom
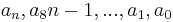= Koeffizienten
n = Grad des Polynom
Nullstellen bestimmen:
f(x)=0
1. Polynomdivision:
Bei Funktionen mindestens dritten Grades und sowohl geraden als auch ungeraden Exponenten, muss zur Bestimmung der Nullstellen eine Polynomdivision durchgefuehrt werden.
Vorgehensweise:
a) Bestimmung einer Nullstelle (N) der Funktion f(x) durch Erraten.
Tipp: als erstes immer für N = -3; -2; -1; 0; 1; 2; 3 einsetzen, da dass die gaengigen Nullstellen sind
b) Erstellung des Termes p(x) = (x - N) durch die soeben gefundene Nullstelle.
c) Nun vereinfacht man die Funktion durch den Bruch :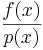
und setzt diesen = 0. Um dies jetzt zu lösen, geht man vor wie bei einer längeren Division.
2. Substitution:
Bei Gleichungen mit Exponente, die aus einer Zahlenreihe kommen. Damit ist beispielsweise 0, 2, 4, 6, 8 oder 3, 6, 9 gemeint.
Beispiel:
Funktion: f(x) =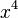 
+ 
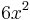+ 8 = 0.
substituiere: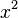 
= z
neue Funktion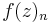 
= 
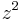+ 6z + 8 = 0.
Nun lässt sich durch die p/q - Formel oder die quadratische Ergänzung die Nullstellen errechnen.
Schließlich wird die Substitution wieder rückgängig gemacht, indem man aus z +/- die Wurzel zieht.
3. p/q-Formel:
f(x) = 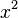+ px + q = 0
= 
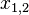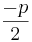
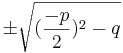
Verhalten von ganzrationalen Funktionen :
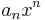: für 
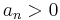gilt
4. quadratische Ergänzung:
Statt die p/q-Formel anzuwenden, können auch mithilfe der quadratischen Ergänzung Nullstellen von einer quadratischen Funktion bestimmt werden.
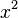+ ax = 
- 
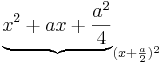