Intergrationsmethoden.: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 1: | Zeile 1: | ||
1. Partielle Integration: | 1. Partielle Integration: | ||
| + | |||
<math> | <math> | ||
\int_{a}^b \mathrm f(x)* g'(x)\,\mathrm dx =[f(x)* g(x)]_a^b- \int_{a}^b \mathrm f'(x)*g(x)\,\mathrm dx | \int_{a}^b \mathrm f(x)* g'(x)\,\mathrm dx =[f(x)* g(x)]_a^b- \int_{a}^b \mathrm f'(x)*g(x)\,\mathrm dx | ||
</math> | </math> | ||
| + | |||
Diese Regel ist insbesondere dann von Vorteil, wenn durch Ableiten von f eine einfachere Funktion entsteht. | Diese Regel ist insbesondere dann von Vorteil, wenn durch Ableiten von f eine einfachere Funktion entsteht. | ||
| Zeile 9: | Zeile 11: | ||
<math>\int_{a}^b \mathrm v(u(x))*u'(x)\,\mathrm dx=\int_{a}^b \mathrm v(z)\,\mathrm dz</math> | <math>\int_{a}^b \mathrm v(u(x))*u'(x)\,\mathrm dx=\int_{a}^b \mathrm v(z)\,\mathrm dz</math> | ||
| + | |||
Bei dieser Regel wird durch die Einführung einer neuen Integrationsvariablen ein Teil des Integranden ersetzt, um das Integral zu vereinfachen. | Bei dieser Regel wird durch die Einführung einer neuen Integrationsvariablen ein Teil des Integranden ersetzt, um das Integral zu vereinfachen. | ||
Version vom 6. Januar 2010, 20:45 Uhr
1. Partielle Integration:
![\int_{a}^b \mathrm f(x)* g'(x)\,\mathrm dx =[f(x)* g(x)]_a^b- \int_{a}^b \mathrm f'(x)*g(x)\,\mathrm dx](/images/math/5/8/9/589ca0cf929acaf134f31a8219cc1efd.png)
Diese Regel ist insbesondere dann von Vorteil, wenn durch Ableiten von f eine einfachere Funktion entsteht.
2. Substitution:
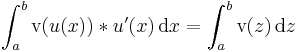
Bei dieser Regel wird durch die Einführung einer neuen Integrationsvariablen ein Teil des Integranden ersetzt, um das Integral zu vereinfachen.
Aufgabenbeispiele
Aufgabenteil d) Substitution
Aufgabenteil d) partielle Integration
Aufgabenteil d) partielle Integration
Aufgabenteil c) Substitution

