Schnitte von Geraden und Ebenen.: Unterschied zwischen den Versionen
Aus KAS-Wiki
(seiteninterne Links) |
|||
| Zeile 1: | Zeile 1: | ||
| − | == | + | == Gegenseitige Lage von zwei Geraden == |
| − | Für zwei Geraden im Raum sind <u>4 Fälle</u> möglich: | + | Für zwei Geraden im Raum sind <u>4 Fälle</u> möglich: |
| + | |||
Sie sind parallel, sie sind identisch, sie schneiden oder sie sind windschief. | Sie sind parallel, sie sind identisch, sie schneiden oder sie sind windschief. | ||
Durch die <u>Richtungsvektoren</u> kann man erkennen, ob die Geraden parallel sind oder nicht. Im Weiteren untersucht man dann die <u>Schnittpunkte</u> der Geraden. | Durch die <u>Richtungsvektoren</u> kann man erkennen, ob die Geraden parallel sind oder nicht. Im Weiteren untersucht man dann die <u>Schnittpunkte</u> der Geraden. | ||
| − | 1. Fall g<math>\|</math>h | + | 1. Fall: g<math>\|</math>h |
| − | + | :a) Stützvektor von g liegt nicht auf h <math>\Rightarrow</math> g und h sind parallel ([[#Beispiel 1|Beispiel 1]]) | |
| − | + | :b) Stützvektor von g liegt auf h <math>\Rightarrow</math> g und h sind identisch ([[#Beispiel 2|Beispiel 2]]) | |
| − | 2. Fall g und h sind nicht parallel | + | 2. Fall: g und h sind nicht parallel |
| − | + | :a) Das LGS hat eine Lösung <math>\Rightarrow</math> g und h schneiden sich ([[#Beispiel 3|Beispiel 3]]) | |
| − | + | :b) Das LGS hat keine Lösung <math>\Rightarrow</math> g und h sind windschief ([[#Beispiel 4|Beispiel 4]]) | |
| − | + | === Beispiel 1 === | |
Bestimmen Sie die gegenseitige Lage der Geraden g und h | Bestimmen Sie die gegenseitige Lage der Geraden g und h | ||
g: <math>\vec x</math>=<math>\begin{pmatrix} 4 \\ -3 \\ 1 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}</math> h: <math>\vec x</math>=<math>\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 6 \\ -3 \\ -9 \end{pmatrix}</math> | g: <math>\vec x</math>=<math>\begin{pmatrix} 4 \\ -3 \\ 1 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}</math> h: <math>\vec x</math>=<math>\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 6 \\ -3 \\ -9 \end{pmatrix}</math> | ||
| − | '''Lösung:''' | + | '''Lösung:''' |
| − | Der Richtungsverktor von h ist das (-3)fache des Richtungsvektors von g <math>\Rightarrow</math> 1. Fall | + | |
| + | Der Richtungsverktor von h ist das (-3)fache des Richtungsvektors von g <math>\Rightarrow</math> | ||
| + | |||
| + | 1. Fall | ||
| + | |||
Man setzt nun den Stützvektor von g gleich der Geraden h. | Man setzt nun den Stützvektor von g gleich der Geraden h. | ||
<math>\begin{pmatrix} 4 \\ -3 \\ 1 \end{pmatrix}</math>=<math>\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 6 \\ -3 \\ -9 \end{pmatrix}</math> | <math>\begin{pmatrix} 4 \\ -3 \\ 1 \end{pmatrix}</math>=<math>\begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 6 \\ -3 \\ -9 \end{pmatrix}</math> | ||
| Zeile 27: | Zeile 32: | ||
Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel. | Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel. | ||
| − | + | === Beispiel 2 === | |
| − | + | === Beispiel 3 === | |
| − | + | === Beispiel 4 === | |
Version vom 7. Dezember 2009, 17:44 Uhr
Inhaltsverzeichnis |
Gegenseitige Lage von zwei Geraden
Für zwei Geraden im Raum sind 4 Fälle möglich:
Sie sind parallel, sie sind identisch, sie schneiden oder sie sind windschief.
Durch die Richtungsvektoren kann man erkennen, ob die Geraden parallel sind oder nicht. Im Weiteren untersucht man dann die Schnittpunkte der Geraden.
1. Fall: g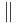 h
h
- a) Stützvektor von g liegt nicht auf h
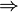 g und h sind parallel (Beispiel 1)
g und h sind parallel (Beispiel 1)
- b) Stützvektor von g liegt auf h
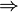 g und h sind identisch (Beispiel 2)
g und h sind identisch (Beispiel 2)
2. Fall: g und h sind nicht parallel
- a) Das LGS hat eine Lösung
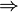 g und h schneiden sich (Beispiel 3)
g und h schneiden sich (Beispiel 3)
- b) Das LGS hat keine Lösung
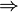 g und h sind windschief (Beispiel 4)
g und h sind windschief (Beispiel 4)
Beispiel 1
Bestimmen Sie die gegenseitige Lage der Geraden g und h
g:  =
=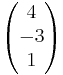 + r
+ r
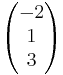 h:
h:  =
=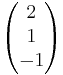 + s
+ s
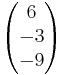
Lösung:
Der Richtungsverktor von h ist das (-3)fache des Richtungsvektors von g 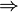
1. Fall
Man setzt nun den Stützvektor von g gleich der Geraden h.
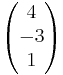 =
=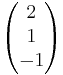 + s
+ s
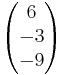 Daraus folgt s =
Daraus folgt s = Setzt man s wieder ein, folgt daraus -3
Setzt man s wieder ein, folgt daraus -3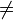 1 +
1 + 
 (-3)
Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel.
(-3)
Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel.

