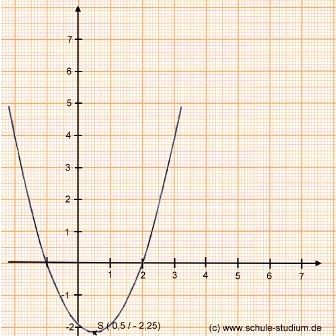
G10: Strecken und Verschieben der Normalparabel: f(x)=a(x-d)²+e

Ein hüpfender Ball beschreibt – wenn man den Reibungsverlust vernachlässigt – Parabelbögen.

Springbrunnen können ebenfalls Parabeln beschreiben.

Definition

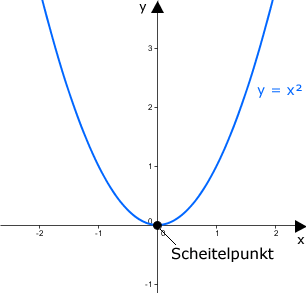
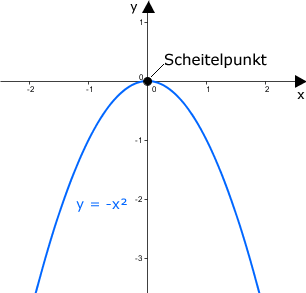
Eine Parabel kann entweder nach oben oder nach unten geöffnet, gestreckt oder gestaucht und entlang der x-Achse und der y-Achse eines Koordinatensystems verschoben sein. Die Verschiebung der Normalparabel kann durch den Scheitelpunkt abgelesen werden. Dies ist der Punkt, in dem die Parabel ihren kleinsten Funktionswert (wenn sie nach oben geöffnet ist) bzw. größten Funktionswert (wenn sie nach unten geöffnet ist) annimmt.

Nach oben geöffnet

Nach unten geöffnet

Funktionsgleichung

Die Funktionsgleichung einer Parabel lautet: f(x)=a(x-d)²+e

• a steht für die Streckung bzw. Stauchung. Ist der Wert größer als 1, ist die Parabel gestreckt, liegt der Wertt zwischen 1 und -1, ist die Parabel gestaucht.
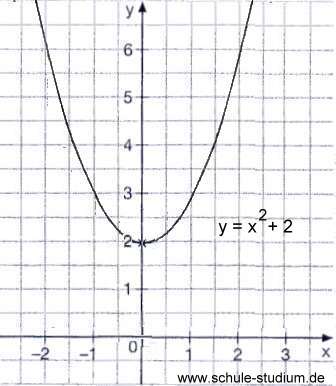
• e steht für die Verschiebung entlang der y-achse
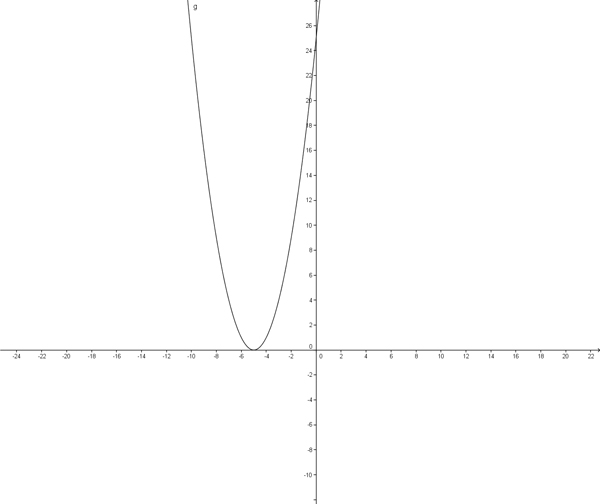
• d steht für die Verschiebung entlang der x-Achse

Beachte:

• Steht ein Minus vor dem Wert d, wird die Parabel auf der x-Achse nach rechts verschoben, steht ein Plus vor dem Wert d, wird die Parabel auf der x-Achse nach links verschoben.
• a darf nicht den Wert 0 besitzen
• d und e dürfen den Wert 0 besitzen
  

Der Scheitelpunkt wird in folgender Form angegeben: (-d|e)

Beispiele:

von Paul und Johannes