Rotationsintegrale.: Unterschied zwischen den Versionen
| Zeile 32: | Zeile 32: | ||
Bei der Rotation um die y-Achse berechnen wir nun den Rotationskörper, der durch die Rotierung der Fläche A um die y-Achse entsteht. Die Fläche A wird durch einen Graphen, die y-Achse und den Gleichungen y=c und y=d begrenzt. | Bei der Rotation um die y-Achse berechnen wir nun den Rotationskörper, der durch die Rotierung der Fläche A um die y-Achse entsteht. Die Fläche A wird durch einen Graphen, die y-Achse und den Gleichungen y=c und y=d begrenzt. | ||
| − | Um das Volumen zu bestimmen, muss der Graph an der Winkelhalbierenden der Kooardinatenachsen gespiegelt werden. In der Rechnung | + | Um das Volumen zu bestimmen, muss der Graph an der Winkelhalbierenden der Kooardinatenachsen gespiegelt werden. In der Rechnung muss man hierzu die Umkehrfunktion bestimmen. [[http://www.oberprima.com/index.php/umkehrfunktion/nachhilfe| Bestimmung von Umkehrfunktionen]] |
| + | |||
| + | Daraus ergibt sich die Volumenformel: | ||
| + | <math>V(y)=\pi\int\limits_{f(a)}^{f(b)}(\bar{f}(y))^2dy</math> | ||
| + | |||
| + | |||
| + | '''Beispiel:''' (''Rauminhalt eines Rotationskörpers bei Rotation um die y-Achse''): | ||
| + | Der Graph der Funktion f mit f(x)= <math>\frac{1}{4}x^2+1</math> begrenzt mit der y-Achse und den Geraden mit den Gleichungen y=2 und y=3 eine Fläche, die um die y-Achse rotiert. | ||
| + | Das Volumen des Rotationskörpers berechnen wir so: | ||
| + | |||
| + | ''Umkehrfunktion bestimmen:'' <math>x^2=(\bar{f}(y))^2 =4y-4</math>, dann gilt | ||
| + | |||
| + | |||
| + | <math>V=\pi\int_2^3(\bar{f}(y))^2dy=\pi\int_2^3(4y-4)dy</math> | ||
| + | |||
| + | <math>=\pi[2y^2-4y]^3_2=6\pi=18.85</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Rotationsintegrale üben == | ||
| + | |||
| + | |||
| + | - ''im Buch(Analysis):'' S. 147-151 | ||
| + | |||
| + | - ''Aufgaben online'':[http://www.klassenarbeiten.net/klassenarbeiten/uebungen/klasse10/mathematik/zylinder_kegel_kugel/rotationskoerper.shtml| Klassenarbeitsübungen] | ||
Version vom 18. Dezember 2009, 11:31 Uhr
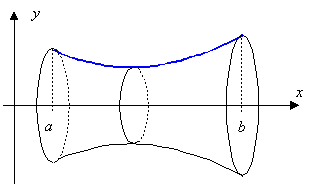
Ein Rotationskörper ensteht, indem man eine Fläche um eine Drehachse rotieren lässt. Diese Fläche ist durch eine auf dem Intervall [a; b] stetige Funktion f, den Gleichungen x=a und x=b und der jeweiligen Achse eingeschlossen.
In der obenstehenden Abbildung handelt es sich, um eine Rotation um die x-Achse. Unser Ziel ist es das Volumen der Rotationskörper bei Rotierung um die x- bzw. y-Achse zu berechnen.
1. Rotation um die x-Achse
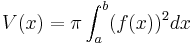
Beispiel (Rauminhalt eines Rotationskörpers bei Rotation um die x-Achse):
Wir haben den Graph der Funktion f mit f(x)=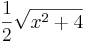
. Dieser begrenzt mit den Koordinatenachsen und der Geraden mit der Gleichung x=4 eine Fläche.
Das Volumen berechnet man so:
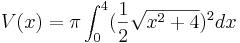
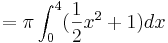
![=\pi[\frac 1{12}x^3+x]^4_0](/images/math/b/f/d/bfdecf26052dccddd6734b4a40bfac3f.png)
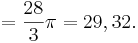
2. Rotation um die y-Achse
Bei der Rotation um die y-Achse berechnen wir nun den Rotationskörper, der durch die Rotierung der Fläche A um die y-Achse entsteht. Die Fläche A wird durch einen Graphen, die y-Achse und den Gleichungen y=c und y=d begrenzt. Um das Volumen zu bestimmen, muss der Graph an der Winkelhalbierenden der Kooardinatenachsen gespiegelt werden. In der Rechnung muss man hierzu die Umkehrfunktion bestimmen. [Bestimmung von Umkehrfunktionen]
Daraus ergibt sich die Volumenformel:
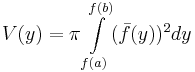
Beispiel: (Rauminhalt eines Rotationskörpers bei Rotation um die y-Achse):
Der Graph der Funktion f mit f(x)=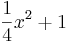 
begrenzt mit der y-Achse und den Geraden mit den Gleichungen y=2 und y=3 eine Fläche, die um die y-Achse rotiert.
Das Volumen des Rotationskörpers berechnen wir so:
Umkehrfunktion bestimmen: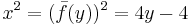 
, dann gilt
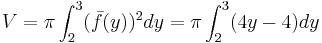
![=\pi[2y^2-4y]^3_2=6\pi=18.85](/images/math/9/4/3/9435b287fda60c6c801154bcbcd25f18.png)
Rotationsintegrale üben
- im Buch(Analysis): S. 147-151
- Aufgaben online:Klassenarbeitsübungen
