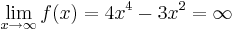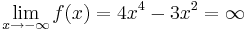Kurvendiskussion: Unterschied zwischen den Versionen
(→Sattelpunkt) |
Enrico (Diskussion | Beiträge) |
||
| (21 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Bei den meisten Funktionen gilt <math>\mathbb{D}</math>=<math>\mathbb{R}</math> | Bei den meisten Funktionen gilt <math>\mathbb{D}</math>=<math>\mathbb{R}</math> | ||
| − | Ausnahmen gibt es bei [[gebrochene rationale Funktionen]] | + | Ausnahmen gibt es bei [[gebrochene rationale Funktionen|gebrochenen rationalen Funktionen]] |
== Symmetrie == | == Symmetrie == | ||
| Zeile 9: | Zeile 9: | ||
=== Punktsymmetrie === | === Punktsymmetrie === | ||
| − | <math>f(-x)=-f(x)</math> | + | <math>f\!(-x)=-f\!(x)</math> |
In der Funktion gibt es nur '''ungerade''' Exponenten | In der Funktion gibt es nur '''ungerade''' Exponenten | ||
| − | |||
=== Achsensymmetrie === | === Achsensymmetrie === | ||
| − | <math>f(-x)=f(x)</math> | + | <math>f\!(-x)=f\!(x)</math> |
In der Funktion gibt es nur '''gerade''' Exponenten | In der Funktion gibt es nur '''gerade''' Exponenten | ||
| + | |||
| + | === Keine Symmetrie === | ||
| + | |||
| + | Die Funktion enthält '''gerade''' als auch '''ungerade''' Exponenten | ||
| + | |||
| + | == Verhalten für hohe x-Beträge == | ||
| + | |||
| + | Ist die Zahl vor dem höchsten Exponent '''positiv''' und der Exponent '''gerade''' so verläuft die Funktion von | ||
| + | "'''links oben nach rechts oben'''" | ||
| + | |||
| + | Ist die Zahl vor dem höchsten Exponent '''negativ''' und der Exponent '''gerade''' so verläuft die Funktion von | ||
| + | "'''links unten nach rechts unten'''" | ||
| + | |||
| + | Ist die Zahl vor dem höchsten Exponent '''positiv''' und der Exponent '''ungerade''' so verläuft die Funktion von | ||
| + | "'''links unten nach rechts oben'''" | ||
| + | |||
| + | Ist die Zahl vor dem höchsten Exponent '''negativ''' und der Exponent '''ungerade''' so verläuft die Funktion von | ||
| + | "'''links oben nach rechts unten'''" | ||
== Nullstellen == | == Nullstellen == | ||
| Zeile 23: | Zeile 40: | ||
Nullstellen sind die Schnittpunkte der Funktion mit der X-Achse. | Nullstellen sind die Schnittpunkte der Funktion mit der X-Achse. | ||
| − | <math>f(x)=0</math> | + | <math>f\!(x)=0</math> |
Der Grad der Funktion gibt die höchst mögliche Anzahl der Nullstellen an. | Der Grad der Funktion gibt die höchst mögliche Anzahl der Nullstellen an. | ||
| Zeile 77: | Zeile 94: | ||
| − | <math>f\!\,'''(x)\not=0</math> | + | <math>f\!\,''(x)=0 \quad \vee \quad f\!\,'''(x)\not=0</math> |
Um die Y-Werte zu berechnen, setzt man die X-Werte in die Funktion <math>f\!(x)</math> ein. | Um die Y-Werte zu berechnen, setzt man die X-Werte in die Funktion <math>f\!(x)</math> ein. | ||
| Zeile 88: | Zeile 105: | ||
== Grenzwertverhalten == | == Grenzwertverhalten == | ||
| + | |||
| + | Das Grenzwertverhalten beschreibt den Verlauf des Graphen bei unendlich großen bzw. kleinen X-Werten. | ||
| + | |||
| + | |||
| + | <math>\lim_{x \to \infty}f(x)</math> | ||
| + | |||
| + | |||
| + | |||
| + | <math>\lim_{x \to -\infty}f(x)</math> | ||
== Zeichnen == | == Zeichnen == | ||
| + | |||
| + | == Beispiel == | ||
| + | |||
| + | <math>f\!(x)=4x^4-3x^2</math> | ||
| + | |||
| + | |||
| + | === Definitionsbereich === | ||
| + | |||
| + | <math>\mathbb{D}=\mathbb{R}</math> | ||
| + | |||
| + | |||
| + | === Symmetrie === | ||
| + | <math>f\!(-x)=4(-x)^4-3(-x)^2</math> | ||
| + | |||
| + | <math>f\!(-x)=4x^4-3x^2</math> | ||
| + | |||
| + | |||
| + | <math>\Rightarrow</math> achsensymmetrisch | ||
| + | |||
| + | |||
| + | Beide Exponenten sind gerade, also ist die Funktion achsensymmetrisch. | ||
| + | |||
| + | === Nullstellen === | ||
| + | |||
| + | <math>\!4x^4-3x^2=0 \quad \textrm{ Substitution: } \quad\!x^2=z</math> | ||
| + | |||
| + | <math>\!4z^2-3z=0</math> | ||
| + | |||
| + | <math>\!z(4z-3)=0</math> | ||
| + | |||
| + | <math>\!z=0 \quad \vee \quad 4z-3=0</math> | ||
| + | |||
| + | <math>\!z=0 \quad \vee \quad 4z=3</math> | ||
| + | |||
| + | <math>\!z=0 \quad \vee \quad z=\frac 34</math> | ||
| + | |||
| + | <math>\!x^2=0 \quad \vee \quad x^2=\frac 34</math> | ||
| + | |||
| + | <math>\!x_1=0 \quad \vee \quad x_2=\sqrt{\frac 34}\quad \vee \quad x_3=-\sqrt{\frac 34}</math> | ||
| + | |||
| + | === Ableitungen === | ||
| + | |||
| + | 1. Ableitung: | ||
| + | |||
| + | <math>f\!\,'(x)=16x^3-6x</math> | ||
| + | |||
| + | |||
| + | 2. Ableitung | ||
| + | |||
| + | <math>f\!\,''(x)=48x^2-6</math> | ||
| + | |||
| + | |||
| + | 3. Ableitung | ||
| + | |||
| + | <math>f\!\,'''(x)=96x</math> | ||
| + | |||
| + | === Extrempunkte === | ||
| + | |||
| + | Notwendige Bedingung: <math>f\!\,'(x)=0</math> | ||
| + | |||
| + | <math>\!16x^3-6x=0</math> | ||
| + | |||
| + | <math>\!x(16x^2-6)=0</math> | ||
| + | |||
| + | <math>\!x_1=0 \quad \vee \quad 16x^2-6=0</math> | ||
| + | |||
| + | <math>\!x_1=0 \quad \vee \quad 16x^2=6</math> | ||
| + | |||
| + | <math>\!x_1=0 \quad \vee \quad x^2=\frac 38</math> | ||
| + | |||
| + | <math>\!x_1=0 \quad \vee \quad x_2=\sqrt{\frac 38}\quad \vee \quad x_3=-\sqrt{\frac 38}</math> | ||
| + | |||
| + | Hinreichende Bedingung: <math>f\!\,''(x)\not=0</math> | ||
| + | |||
| + | <math>f\!\,''(0)=48*0-6=-6 \quad \Rightarrow \quad Maximum</math> | ||
| + | |||
| + | <math>f\!\,''(\sqrt{\frac 38})=48*\frac38-6=12 \quad \Rightarrow \quad Minimum</math> | ||
| + | |||
| + | <math>f\!\,''(-\sqrt{\frac 38})=48*\frac38-6=12 \quad \Rightarrow \quad Minimum</math> | ||
| + | === Wendepunkte === | ||
| + | |||
| + | Notwendige Bedingung: <math>f\!\,''(x)=0</math> | ||
| + | |||
| + | <math>\!48x^2-6=0</math> | ||
| + | |||
| + | <math>\!48x^2=6</math> | ||
| + | |||
| + | <math>\!x^2=\frac18</math> | ||
| + | |||
| + | <math>x_1=\sqrt{\frac18}\quad \vee \quad x_2=\sqrt{-\frac 18}</math> | ||
| + | |||
| + | Hinreichende Bedingung: <math>f\!\,'''(x)\not=0</math> | ||
| + | |||
| + | <math>f\!\,'''(\sqrt{\frac18})=96*\sqrt{\frac18}=24*\sqrt{2}</math> | ||
| + | |||
| + | <math>f\!\,'''(-\sqrt{\frac18})=96*-\sqrt{\frac18}=-24*\sqrt{2}</math> | ||
| + | |||
| + | === Grenzwertverhalten === | ||
| + | |||
| + | <math>\lim_{x \to \infty}f(x)=4x^4-3x^2=\infty</math> | ||
| + | |||
| + | <math>\lim_{x \to -\infty}f(x)=4x^4-3x^2=\infty</math> | ||
| + | [[Kategorie:Kurvendiskussion|!]] | ||
<!-- In der Wiki-Family --> | <!-- In der Wiki-Family --> | ||
Aktuelle Version vom 19. April 2012, 14:28 Uhr
Inhaltsverzeichnis |
Definitionsbereich
Bei den meisten Funktionen gilt 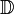 =
=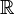
Ausnahmen gibt es bei gebrochenen rationalen Funktionen
Symmetrie
Punktsymmetrie

In der Funktion gibt es nur ungerade Exponenten
Achsensymmetrie
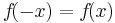
In der Funktion gibt es nur gerade Exponenten
Keine Symmetrie
Die Funktion enthält gerade als auch ungerade Exponenten
Verhalten für hohe x-Beträge
Ist die Zahl vor dem höchsten Exponent positiv und der Exponent gerade so verläuft die Funktion von "links oben nach rechts oben"
Ist die Zahl vor dem höchsten Exponent negativ und der Exponent gerade so verläuft die Funktion von "links unten nach rechts unten"
Ist die Zahl vor dem höchsten Exponent positiv und der Exponent ungerade so verläuft die Funktion von "links unten nach rechts oben"
Ist die Zahl vor dem höchsten Exponent negativ und der Exponent ungerade so verläuft die Funktion von "links oben nach rechts unten"
Nullstellen
Nullstellen sind die Schnittpunkte der Funktion mit der X-Achse.
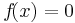
Der Grad der Funktion gibt die höchst mögliche Anzahl der Nullstellen an.
Ableitungen
1. Ableitung 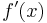
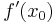 gibt die Steigung m im Punkt
gibt die Steigung m im Punkt 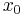 an.
an.
2. Ableitung 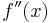
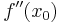 gibt die Krümmung von
gibt die Krümmung von 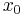 an.
Bei positiven Werten handelt es sich um eine Rechtskrümmung, bei negativen Werten um eine Linkskrümmung.
an.
Bei positiven Werten handelt es sich um eine Rechtskrümmung, bei negativen Werten um eine Linkskrümmung.
3. Ableitung 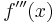
Zur Berechnung: siehe Ableitungsregeln
Extrempunkte
In Extrempunkten (Hoch- und Tiefpunkten) ist die Steigung m=0
also ist die notwendige Bedingung:
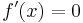
Die erhaltenen X-Werte setzt man nun in der hinreichenden Bedingung in die zweite Ableitung ein:
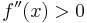 hierbei handelt es sich um eine Linkskrümmung, also um ein Minimum.
hierbei handelt es sich um eine Linkskrümmung, also um ein Minimum.
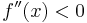 hierbei handelt es sich um eine Rechtskrümmung, also um ein Maximum.
hierbei handelt es sich um eine Rechtskrümmung, also um ein Maximum.
Um die Y-Werte der Hoch- bzw. Tiefpunkte zu erhalten, setzt man die X-Werte in die Ursprungsfunktion 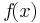 ein.
ein.
Wendepunkte
In einem Wendepunkt wechselt die Krümmung zwischen links und rechts. Folglich ist die Krümmung, also die zweite Ableitung in diesem Punkt 0
Notwendige Bedingung
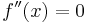
zusätzlich muss auch die hinreichende Bedingung erfüllt sein, um zu garantieren, dass es sich um einen Wendepunkt handelt:
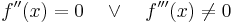
Um die Y-Werte zu berechnen, setzt man die X-Werte in die Funktion 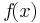 ein.
ein.
Sattelpunkt
Bei einem Sattelpunkt handelt es sich um einen besonderen Wendepunkt, da es zu diesem Punkt eine waagerechte Tangente gibt. Folglich ist hier die Steigung m=0
Grenzwertverhalten
Das Grenzwertverhalten beschreibt den Verlauf des Graphen bei unendlich großen bzw. kleinen X-Werten.
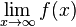
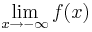
Zeichnen
Beispiel
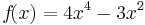
Definitionsbereich
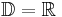
Symmetrie
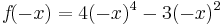
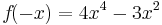
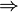 achsensymmetrisch
achsensymmetrisch
Beide Exponenten sind gerade, also ist die Funktion achsensymmetrisch.
Nullstellen
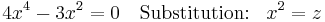
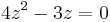
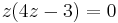

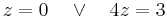


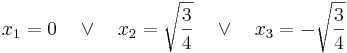
Ableitungen
1. Ableitung:

2. Ableitung
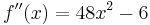
3. Ableitung
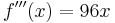
Extrempunkte
Notwendige Bedingung: 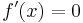
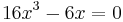
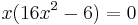
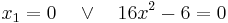
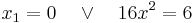

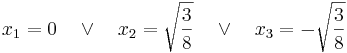
Hinreichende Bedingung: 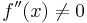
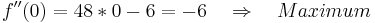
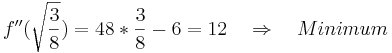
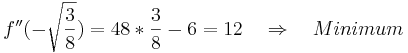
Wendepunkte
Notwendige Bedingung: 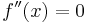
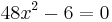
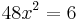
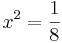
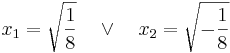
Hinreichende Bedingung: 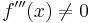
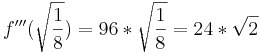
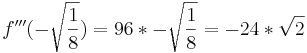
Grenzwertverhalten