Rotationsintegrale: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 10: | Zeile 10: | ||
<math>V(y)=\pi*\int\limits_{f(a)}^{f(b)}(f^{-1}(y))^2dy</math> | <math>V(y)=\pi*\int\limits_{f(a)}^{f(b)}(f^{-1}(y))^2dy</math> | ||
| − | Anwendung am Beispiel <math>0, | + | |
| + | |||
| + | == Anwendung am Beispiel == | ||
| + | <math>0,5*\sqrt{x^2+4}</math> im Intervall [0;2]. | ||
| + | |||
| + | Zunächst wird | ||
Version vom 1. Dezember 2009, 12:46 Uhr
Rotationsintegral(Volumen von Rotationskörpern)
Das Volumen des Körpers bei der Rotation der Flächen zwischen dem Graphen von f und der x-Achse im Intervall [a;b].
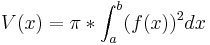
Das Volumen des Körpers bei der Rotation der Flächen zwischen dem Graphen von f und der y-Achse im Intervall[a;b]. Dabei sei f umkehrbar mit 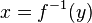 .
.
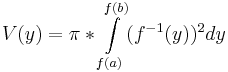
Anwendung am Beispiel
im Intervall [0;2].
Zunächst wird

