Exponentielles Wachstum: Unterschied zwischen den Versionen
Aus KAS-Wiki
Martin (Diskussion | Beiträge) |
Martin (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). | Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). | ||
Die Proportionalitätskonstante ist die Wachstumskonstante k. | Die Proportionalitätskonstante ist die Wachstumskonstante k. | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<math>f'(x)=k*f(x)</math> | <math>f'(x)=k*f(x)</math> | ||
Die Lösung dieser Differenzialgleichung ist: | Die Lösung dieser Differenzialgleichung ist: | ||
<math>f(x)=c*e^{kt}</math> | <math>f(x)=c*e^{kt}</math> | ||
| + | |||
| + | Dies kann z.B. so formuliert sein: | ||
| + | -Der vorhandene Wert nimmt immer um 10% zu. K wäre dann also ln(1,1). (k=ln(1+p%)) | ||
| + | -Turiner Grabtuch: <sup>14</sup>C-Methode + Halbwertszeit 5730 Jahre -> keine Schranke | ||
| + | => exponentielles Wachstum | ||
| + | <math>k=-\frac{ln(2)}{5730}</math> | ||
| + | -Abbau radioaktiver Substanzen:Ein Kontrastmittel wird von der Leber mit einer Rate abgebaut, | ||
| + | die proportional zur vorhandenen Menge des Kontrastmittels ist. | ||
| + | => exponentielles Wachstum (Angabe zu Mengen: f(0)=0,75 & f(2)=0,747 daraus ergibt sich k) | ||
Aktuelle Version vom 15. Februar 2011, 13:03 Uhr
Die Änderungsrate des exponentiellen Wachstums ist proportional zur Wachstumsfunktion f(x). Die Proportionalitätskonstante ist die Wachstumskonstante k.
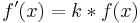
Die Lösung dieser Differenzialgleichung ist:
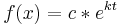
Dies kann z.B. so formuliert sein:
-Der vorhandene Wert nimmt immer um 10% zu. K wäre dann also ln(1,1). (k=ln(1+p%))
-Turiner Grabtuch: 14C-Methode + Halbwertszeit 5730 Jahre -> keine Schranke
=> exponentielles Wachstum
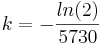-Abbau radioaktiver Substanzen:Ein Kontrastmittel wird von der Leber mit einer Rate abgebaut,
die proportional zur vorhandenen Menge des Kontrastmittels ist.
=> exponentielles Wachstum (Angabe zu Mengen: f(0)=0,75 & f(2)=0,747 daraus ergibt sich k)
