Scheitelpunkt berechnen: Unterschied zwischen den Versionen
Aus KAS-Wiki
Arman1 (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „'''Scheitelpunkt berechnen''' ''Beispiel'' <math>f(x)=x^2+6x+5</math> |Quadratische Ergänzung <math>f(x)=x^2+6x+9-9+5</math>“) |
|||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | '''Scheitelpunkt berechnen''' | + | '''Scheitelpunkt berechnen'''<sup>Hochgestellt</sup> |
| − | ''Beispiel'' | + | ''Beispiel:''[http://www.example.com Link-Text] |
<math>f(x)=x^2+6x+5</math> | <math>f(x)=x^2+6x+5</math> | ||
| − | |||
| + | Dann macht man eine quadratische ergänzung: | ||
<math>f(x)=x^2+6x+9-9+5</math> | <math>f(x)=x^2+6x+9-9+5</math> | ||
| + | |||
| + | Das ist dann eine binomische Formel: | ||
| + | |||
| + | <math>f(x)=(x+3)^2-9+5</math> | ||
| + | |||
| + | <math>f(x)=(x+3)^2-4</math> | ||
| + | |||
| + | Daraus nimmt man dann den Scheitelpunkt: | ||
| + | |||
| + | <math>S(-3|-4)</math> | ||
| + | |||
| + | |||
| + | ''Weiteres Beispiel'': | ||
| + | |||
| + | Aufgabenstellung: Wie wandelt man '''f(x)= 3x<sup>2</sup>+2x-1''' in die Scheitelpunktsform um? | ||
| + | .. | ||
| + | Rechnung: | ||
| + | |||
| + | |||
| + | f(x)= 3x<sup>2</sup>+2x-1 | :3 | ||
| + | |||
| + | f(x):3=x<sup>2</sup>+2/3x-1/3 | +1/9-1/9 | ||
| + | |||
| + | f(x):3=x<sup>2</sup>+2/3x+1/9-1/9-1/3 | ||
| + | |||
| + | |||
| + | '''2 Möglichkeit:''' | ||
| + | |||
| + | Mann kann die Nullstellen auch mit hilfe der p/q-Formel berechnen. | ||
| + | Die beiden Formeln findest du im Ordner [[p/q-Formel]]. | ||
| + | |||
| + | 3x²+5x+1 = 0 |/3 | ||
| + | |||
| + | x²+1,67x+0,33=0 | ||
| + | |||
| + | p=1,67 | ||
| + | |||
| + | q=0,33 | ||
| + | |||
| + | Diese beiden Punkte müssen nur noch in die p/q Formel eingesetzt werden und man hat den Scheitelpunkt. | ||
| + | |||
| + | |||
| + | 3 Möglichkeit: Der Satz von vieta | ||
| + | |||
| + | [http://www.arndt-bruenner.de/mathe/pdf/vieta1.pdf] | ||
Aktuelle Version vom 6. Dezember 2011, 11:20 Uhr
Scheitelpunkt berechnenHochgestellt
Beispiel:Link-Text
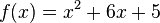
Dann macht man eine quadratische ergänzung:
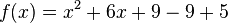
Das ist dann eine binomische Formel:
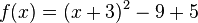
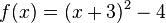
Daraus nimmt man dann den Scheitelpunkt:
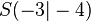
Weiteres Beispiel:
Aufgabenstellung: Wie wandelt man f(x)= 3x2+2x-1 in die Scheitelpunktsform um? .. Rechnung:
f(x)= 3x2+2x-1 | :3
f(x):3=x2+2/3x-1/3 | +1/9-1/9
f(x):3=x2+2/3x+1/9-1/9-1/3
2 Möglichkeit:
Mann kann die Nullstellen auch mit hilfe der p/q-Formel berechnen. Die beiden Formeln findest du im Ordner p/q-Formel.
3x²+5x+1 = 0 |/3
x²+1,67x+0,33=0
p=1,67
q=0,33
Diese beiden Punkte müssen nur noch in die p/q Formel eingesetzt werden und man hat den Scheitelpunkt.
3 Möglichkeit: Der Satz von vieta

