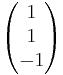Schnitte von Geraden und Ebenen.: Unterschied zwischen den Versionen
(→Beispiel 2.1) |
(Kategorie:Analytische Geometrie) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 112: | Zeile 112: | ||
=== Beispiel 2.2 === | === Beispiel 2.2 === | ||
| − | Untersuchen Sie die gegenseitige Lage der Geraden g: <math>\vec x</math>=<math>\begin{pmatrix} -2 \\ 3 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}</math> | + | Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E.<br /> |
| + | : g: <math>\vec x</math>=<math>\begin{pmatrix} -2 \\ 3 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}</math> E: x<sub>1</sub> - 2x<sub>2</sub> - 3x<sub>3</sub> = 1. | ||
'''Lösung:''' | '''Lösung:''' | ||
Man setzt nun x<sub>1</sub> = -2 + r, x<sub>2</sub> = 3 + 2r und x<sub>3</sub> = 4 - r in die Ebenengleichung ein, dann ergibt sich:<br /> | Man setzt nun x<sub>1</sub> = -2 + r, x<sub>2</sub> = 3 + 2r und x<sub>3</sub> = 4 - r in die Ebenengleichung ein, dann ergibt sich:<br /> | ||
| − | -2 r -2(3 + 2r) - 3(4 - r) = 1 <math>\Rightarrow</math> -20 = 1; Somit sind g und E parallel. | + | :-2 r -2(3 + 2r) - 3(4 - r) = 1 <math>\Rightarrow</math> -20 = 1; Somit sind g und E '''parallel'''. |
=== Beispiel 2.3 === | === Beispiel 2.3 === | ||
| − | Untersuchen Sie die gegenseitige Lage der Geraden g: <math>\vec x</math>=<math>\begin{pmatrix} -3 \\ 4 \\ 1 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix}</math> | + | Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E.<br /> |
| + | :g: <math>\vec x</math>=<math>\begin{pmatrix} -3 \\ 4 \\ 1 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix}</math> E: x<sub>1</sub> - 2x<sub>2</sub> - 3x<sub>3</sub> = 14. | ||
'''Lösung:''' | '''Lösung:''' | ||
Man setzt nun x<sub>1</sub> = -3 + 5r, x<sub>2</sub> = 4 - 2r und x<sub>3</sub> = 1 + 3r in die Ebenengleichung ein, dann ergibt sich:<br /> | Man setzt nun x<sub>1</sub> = -3 + 5r, x<sub>2</sub> = 4 - 2r und x<sub>3</sub> = 1 + 3r in die Ebenengleichung ein, dann ergibt sich:<br /> | ||
| − | -3 + 5r -2(4 - 2r) - 3(1 + 3r) = 14 <math>\Rightarrow</math> 0 = 0; Somit liegt g in E. | + | :-3 + 5r -2(4 - 2r) - 3(1 + 3r) = 14 <math>\Rightarrow</math> 0 = 0; Somit '''liegt g in E'''. |
== '''Gegenseitige Lage von zwei Ebenen''' == | == '''Gegenseitige Lage von zwei Ebenen''' == | ||
| Zeile 142: | Zeile 144: | ||
=== Beispiel 3.1 === | === Beispiel 3.1 === | ||
| − | Untersuchen Sie die gegenseitige Lage der Ebenen E<sub>1</sub>: 3x<sub>1</sub> - 2x<sub>2</sub> + x<sub>3</sub> = 3 und E<sub>2</sub>: 5x<sub>1</sub> + 3x<sub>2</sub> - 2x<sub>3</sub> = 6 | + | Untersuchen Sie die gegenseitige Lage der beiden Ebenen.<br /> |
| + | : E<sub>1</sub>: 3x<sub>1</sub> - 2x<sub>2</sub> + x<sub>3</sub> = 3 und E<sub>2</sub>: 5x<sub>1</sub> + 3x<sub>2</sub> - 2x<sub>3</sub> = 6 | ||
'''Lösung:''' | '''Lösung:''' | ||
| Zeile 154: | Zeile 157: | ||
:x<sub>3</sub> = -21 + 19r | :x<sub>3</sub> = -21 + 19r | ||
| − | Daraus ergibt sich die Schnittgerade: | + | Daraus ergibt sich die '''Schnittgerade''': |
:<math>\vec x</math>=<math>\begin{pmatrix} 0 \\ -12 \\ -21 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 11 \\ 19 \end{pmatrix}</math> | :<math>\vec x</math>=<math>\begin{pmatrix} 0 \\ -12 \\ -21 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 11 \\ 19 \end{pmatrix}</math> | ||
=== Beispiel 3.2 === | === Beispiel 3.2 === | ||
| − | Untersuchen Sie die gegenseitige Lage der Ebenen E<sub>1</sub>: <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ 8 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}</math> | + | Untersuchen Sie die gegenseitige Lage der beiden Ebenen.<br /> |
| + | : E<sub>1</sub>: <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ 8 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}</math> E<sub>2</sub>: <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ -1 \\ -1 \end{pmatrix}</math> + t<math>\cdot</math><math>\begin{pmatrix} 1 \\ -4 \\ -1 \end{pmatrix}</math> + u<math>\cdot</math><math>\begin{pmatrix} -2 \\ 3 \\ 7 \end{pmatrix}</math> | ||
| − | '''Lösung:''' | + | '''Lösung:'''<br /> |
Daraus ergibt sich <math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ 8 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}</math> = <math>\begin{pmatrix} 1 \\ -1 \\ -1 \end{pmatrix}</math> + t<math>\cdot</math><math>\begin{pmatrix} 1 \\ -4 \\ -1 \end{pmatrix}</math> + u<math>\cdot</math><math>\begin{pmatrix} -2 \\ 3 \\ 7 \end{pmatrix}</math> <br /> | Daraus ergibt sich <math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 1 \\ 2 \\ 8 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix}</math> = <math>\begin{pmatrix} 1 \\ -1 \\ -1 \end{pmatrix}</math> + t<math>\cdot</math><math>\begin{pmatrix} 1 \\ -4 \\ -1 \end{pmatrix}</math> + u<math>\cdot</math><math>\begin{pmatrix} -2 \\ 3 \\ 7 \end{pmatrix}</math> <br /> | ||
Man Erhält das LGS:<br /> | Man Erhält das LGS:<br /> | ||
| Zeile 167: | Zeile 171: | ||
: 4 +8r + 2s = -1 -t +7u<br /> | : 4 +8r + 2s = -1 -t +7u<br /> | ||
| − | Daraus folgt, dass das LGS unendlich viele Lösungen hat, d.h. die Ebenen schneiden sich. | + | Daraus folgt, dass das LGS unendlich viele Lösungen hat, d.h. die Ebenen '''schneiden sich'''.<br /> |
| − | Setzt man u in E<sub>2</sub>, erhält man die Schnittgerade:<br /> | + | Setzt man u in E<sub>2</sub>, erhält man die '''Schnittgerade''':<br /> |
| − | math>\vec x</math>=<math>\begin{pmatrix} 2 \\ -2,5 \\ -4,5 \end{pmatrix}</math> + t<math>\cdot</math><math>\begin{pmatrix} 4 \\ -7 \\ -13 \end{pmatrix}</math> | + | <math>\vec x</math>=<math>\begin{pmatrix} 2 \\ -2,5 \\ -4,5 \end{pmatrix}</math> + t<math>\cdot</math><math>\begin{pmatrix} 4 \\ -7 \\ -13 \end{pmatrix}</math> |
=== Beispiel 3.3 === | === Beispiel 3.3 === | ||
| − | Untersuchen Sie die gegenseitige Lage der Ebenen E<sub>1</sub>: x<sub>1</sub> + x<sub>2</sub> 2x<sub>3</sub> = 10 | + | Untersuchen Sie die gegenseitige Lage der beiden Ebenen.<br /> |
| + | : E<sub>1</sub>: x<sub>1</sub> + x<sub>2</sub> 2x<sub>3</sub> = 10; E<sub>2</sub>: <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}</math> + r<math>\cdot</math><math>\begin{pmatrix} 0 \\ 1 \\ -3 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 4 \\ 1 \\ 5 \end{pmatrix}</math> | ||
| − | '''Lösung:''' | + | '''Lösung:'''<br /> |
| − | Setzt man x<sub>1</sub> = 1 + 4s, x<sub>2</sub> = 2 + r + s und x<sub>3</sub> = 1 - 3r + 5s in E<sub>2</sub> ein, erhält man die Gleichung r = 3s - 1; Somit schneiden sich die Ebenen. | + | Setzt man x<sub>1</sub> = 1 + 4s, x<sub>2</sub> = 2 + r + s und x<sub>3</sub> = 1 - 3r + 5s in E<sub>2</sub> ein, erhält man die Gleichung r = 3s - 1; Somit '''schneiden sich''' die Ebenen.<br /> |
| − | Setzt man r in E<sub>2</sub> ein, erhält man die Schnittgerade <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}</math> | + | Setzt man r in E<sub>2</sub> ein, erhält man die '''Schnittgerade''' <math>\vec x</math>=<math>\begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}</math> + s<math>\cdot</math><math>\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}</math> |
== Siehe auch == | == Siehe auch == | ||
* [[Schnitte von Geraden und Ebenen]] | * [[Schnitte von Geraden und Ebenen]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Analytische Geometrie]] | ||
Aktuelle Version vom 27. Dezember 2010, 10:48 Uhr
Inhaltsverzeichnis |
Gegenseitige Lage von zwei Geraden
Für zwei Geraden im Raum sind 4 Fälle möglich:
Sie sind parallel, sie sind identisch, sie schneiden oder sie sind windschief.
Durch die Richtungsvektoren kann man erkennen, ob die Geraden parallel sind oder nicht. Im Weiteren untersucht man dann die Schnittpunkte der Geraden.
1. Fall: g h
h
a) Stützvektor von g liegt nicht auf hg und h sind parallel (Beispiel 1.1)
b) Stützvektor von g liegt auf hg und h sind identisch (Beispiel 1.2)
2. Fall: g und h sind nicht parallel
a) Das LGS hat eine Lösungg und h schneiden sich (Beispiel 1.3)
b) Das LGS hat keine Lösungg und h sind windschief (Beispiel 1.4)
Beispiel 1.1
Bestimmen Sie die gegenseitige Lage der Geraden g und h
- g:
 =
=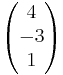 + r
+ r
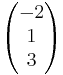 h:
h:  =
=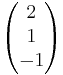 + s
+ s
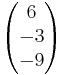
Lösung:
Der Richtungsverktor von h ist das (-3)fache des Richtungsvektors von g 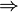 1. Fall
1. Fall
Man setzt nun den Stützvektor von g gleich der Geraden h.
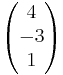 =
=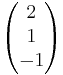 + s
+ s
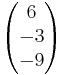
Daraus folgt s = Setzt man s wieder ein, folgt daraus -3
Setzt man s wieder ein, folgt daraus -3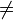 1 +
1 + 
 (-3)
Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel.
(-3)
Somit liegt der Stützvektor nicht auf h und die Geraden sind damit parallel.
Beispiel 1.2
Bestimmen Sie die gegenseitige Lage der Geraden g und h.
- g:
 =
=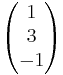 + r
+ r
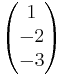 h:
h:  =
=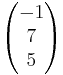 + s
+ s
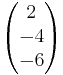
Lösung:
Der Richtungsverktor von h ist das Doppelte des Richtungsvektors von g 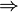 1. Fall
1. Fall
Man setzt nun den Stützvektor von g gleich der Geraden h.
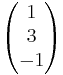 =
= + s
+ s
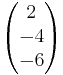
Daraus folgt s = 1
Setzt man s wieder ein, folgt daraus 3=7-4  -1=5-6
Somit liegt der Stützvektor auf h und die Geraden sind damit identisch.
-1=5-6
Somit liegt der Stützvektor auf h und die Geraden sind damit identisch.
Beispiel 1.3
Bestimmen Sie die gegenseitige Lage der Geraden g und h.
- g:
 =
=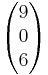 + r
+ r
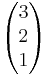 h:
h:  =
=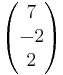 + s
+ s
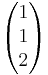
Lösung:
Der Richtungsverktor von h ist kein Vielfaches des Richtungsvektors von g  2. Fall
2. Fall
Man setzt nun die beiden Geraden gleich.
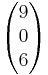 + r
+ r
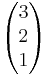 =
= 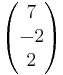 + s
+ s
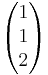
Daraus ergibt sich das LGS:
- 9+3r = 7+ s
- 2r = -2+ s
- 6+ r = 2+2s
Als einzige Lösung ergibt sich r = 0; s = 2
Somit schneiden sich die Geraden g und h. Will man den Schnittpunkt ausrechenen, muss man s und r in eine der Geraden einsetzen.
- Mit r = 0 und s = 2 ergibt sich der Schnittpunkt S(9|0|6)
Beispiel 1.4
Bestimmen Sie die gegenseitige Lage der Geraden g und h.
- g:
 =
=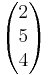 + r
+ r
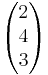 h:
h:  =
=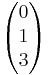 + s
+ s
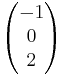
Lösung:
Der Richtungsverktor von h ist kein Vielfaches des Richtungsvektors von g  2. Fall
2. Fall
Man setzt nun die beiden Geraden gleich.
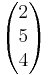 + r
+ r
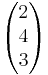 =
= 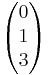 + s
+ s
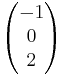
Daraus ergibt sich das LGS:
- 2+2r = -s
- 5+4r = 1
- 4+3r = 3+2s
Dieses LGS hat keine Lösung, somit sind die Geraden windschief.
Gegenseitige Lage einer Geraden und einer Ebene
Für die gegenseitige Lage einer Gerade g und einer Ebene E sind 3 Fälle Möglich:
1) g und E schneiden sich 2) g und E sind parallel 3) g liegt in E
Ist die Ebene E durch eine Koordinatengleichung gegeben, erhält man aus dieser durch Einsetzen von x1, x2 und x3 aus der Geradengleichung eine Gleichung für den Parameter.
Die verschiedenen Lagen von g und E ergeben sich, je nachdem, ob diese Gleichung
- 1) genau eine Lösung (Beispiel 2.1)
- 2) keine Lösung (Beispiel 2.2)
- 3) unendlich viele Lösungen hat (Beispiel 2.3)
Beispiel 2.1
Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E.
- g:
 =
=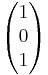 + r
+ r
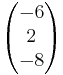 E: -3x1 + x2 - 4x3 = 6.
E: -3x1 + x2 - 4x3 = 6.
Lösung:
Man setzt nun x1 = 1 - 6r, x2 = 2r und x3 = 1 - 8r in die Ebenengleichung ein, dann ergibt sich:
-3(1 - 6r) + 2r - 4(1 - 8t) = 6
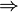 r =
r =  somit schneiden sich g und E.
somit schneiden sich g und E.
Um den Schnittpunkt auszurechnen, setzt man r in g ein 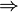 S(-0,5|0,5|-1)
S(-0,5|0,5|-1)
Beispiel 2.2
Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E.
- g:
 =
=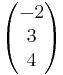 + r
+ r
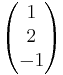 E: x1 - 2x2 - 3x3 = 1.
E: x1 - 2x2 - 3x3 = 1.
Lösung:
Man setzt nun x1 = -2 + r, x2 = 3 + 2r und x3 = 4 - r in die Ebenengleichung ein, dann ergibt sich:
- -2 r -2(3 + 2r) - 3(4 - r) = 1
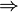 -20 = 1; Somit sind g und E parallel.
-20 = 1; Somit sind g und E parallel.
Beispiel 2.3
Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E.
- g:
 =
=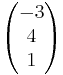 + r
+ r
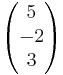 E: x1 - 2x2 - 3x3 = 14.
E: x1 - 2x2 - 3x3 = 14.
Lösung:
Man setzt nun x1 = -3 + 5r, x2 = 4 - 2r und x3 = 1 + 3r in die Ebenengleichung ein, dann ergibt sich:
- -3 + 5r -2(4 - 2r) - 3(1 + 3r) = 14
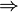 0 = 0; Somit liegt g in E.
0 = 0; Somit liegt g in E.
Gegenseitige Lage von zwei Ebenen
Für die gegenseitige Lage von zwei Ebenen sind 3 Fälle möglich:
1) Sie schneiden sich (Schnittgerade) 2) Sie sind parallel 3) Sie sind identisch
Lageuntersuchung bei verschiedenen Formen der Ebenengleichungen:
- 1) Sind beide Ebenen in Koordinatenform gegeben, fass man diese als LGS mit drei Variablen zusammen (Beispiel 3.1)
- 2) Sind beide Ebenen in Parameterform gegeben, setzt man diese gleich und erhält ein LGS mit drei Gleichungen und vier Variablen (Beispiel 3.2)
- 3) Ist eine Ebene in Parameter- und eine in Koordinatenform gegeben, setzt man x1, x2 und x3 aus der Parametergleichung in die Koordinatengleichung ein und erhält eine Gleichung mit den beiden Variablen (Beispiel 3.3)
Beispiel 3.1
Untersuchen Sie die gegenseitige Lage der beiden Ebenen.
- E1: 3x1 - 2x2 + x3 = 3 und E2: 5x1 + 3x2 - 2x3 = 6
Lösung:
Aus den beiden Gleichungen ergibt sich das LGS:
- 3x1 - 2x2 + x3 = 3
- 5x1 + 3x2 - 2x3 = 6
Da dieses LGS unterbestimmt ist setzt man x1 = r, dann erhält man:
- x1 = r
- x2 = 11r - 12
- x3 = -21 + 19r
Daraus ergibt sich die Schnittgerade:
 =
=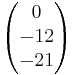 + r
+ r
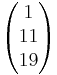
Beispiel 3.2
Untersuchen Sie die gegenseitige Lage der beiden Ebenen.
- E1:
 =
=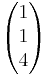 + r
+ r
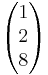 + s
+ s
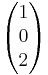 E2:
E2:  =
=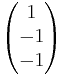 + t
+ t
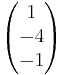 + u
+ u
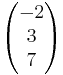
Lösung:
Daraus ergibt sich 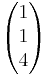 + r
+ r
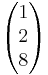 + s
+ s
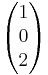 =
= 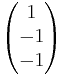 + t
+ t
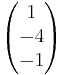 + u
+ u

Man Erhält das LGS:
- 1 + r + s = 1 + t -2u
- 1 + 2r = -1 - 4t + 3u
- 4 +8r + 2s = -1 -t +7u
Daraus folgt, dass das LGS unendlich viele Lösungen hat, d.h. die Ebenen schneiden sich.
Setzt man u in E2, erhält man die Schnittgerade:
 =
=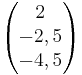 + t
+ t
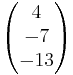
Beispiel 3.3
Untersuchen Sie die gegenseitige Lage der beiden Ebenen.
- E1: x1 + x2 2x3 = 10; E2:
 =
=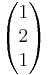 + r
+ r
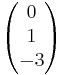 + s
+ s
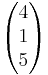
Lösung:
Setzt man x1 = 1 + 4s, x2 = 2 + r + s und x3 = 1 - 3r + 5s in E2 ein, erhält man die Gleichung r = 3s - 1; Somit schneiden sich die Ebenen.
Setzt man r in E2 ein, erhält man die Schnittgerade  =
=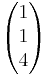 + s
+ s