Schnitte von Geraden und Ebenen
Inhaltsverzeichnis[Verbergen] |
Lagebeziehungen von Geraden und Geraden
Es gibt mehrere Möglichkeiten, wie zwei Geraden im Raum zueinander liegen können.
Sie können identisch, zueinander parallel, sich schneiden oder zueinander windschief sein.
Die zwei Geraden sind definiert durch 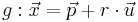 und
und 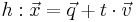
Identisch
Vorraussetzungen:
Die Richtungsvektoren, also  und
und  sind linear abhängig.
sind linear abhängig.
Der Stützvektor von 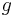 liegt auf der Geraden
liegt auf der Geraden 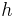 , der SV von
, der SV von 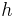 liegt auf der Geraden
liegt auf der Geraden 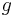 .
.
Identisch sind 2 Geraden also dann, wenn sie auf einer Linie liegen.
Zueinander parallel
Vorraussetzungen:
Die Richtungsvektoren, also 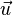 und
und 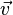 sind linear abhängig.
sind linear abhängig.
Der Stützvektor von 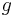 liegt nicht auf der Geraden
liegt nicht auf der Geraden 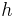 , der SV von
, der SV von 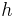 liegt nicht auf der Geraden
liegt nicht auf der Geraden 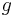 .
.
Schnittpunkt
Vorraussetzungen:
Die Richtungsvektoren sind linear unabhängig.
Wenn man 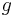 und
und 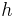 gleichsetzt, erhält man genau eine Lösung.
gleichsetzt, erhält man genau eine Lösung.
Windschief
Vorraussetzungen:
Die Richtungsvektoren sind linear unabhängig.
Wenn man 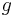 und
und 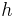 gleichsetzt, erhält man keine Lösung.
gleichsetzt, erhält man keine Lösung.
Lagebeziehungen von Ebenen und Geraden
Eine Ebene und eine Gerade können zueinander parallel oder identisch sein oder sich schneiden.
Gegeben seien die Gerade 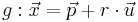 und die Ebene
und die Ebene 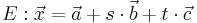
Gerade liegt in der Ebene
Vorraussetzungen:
Der Richtungsvektor der Gerade RVg und die Richtungsvektoren der Ebene RV1 und RV2 sind linear abhängig.
Wenn man 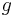 in die Koordinatenform von
in die Koordinatenform von 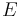 einsetzt, erhält man unendlich viele Lösungen, da es unendlich viele Schnittpunkte gibt. Zum Umformen der Parameterform in die Koordinatenform siehe hier.
einsetzt, erhält man unendlich viele Lösungen, da es unendlich viele Schnittpunkte gibt. Zum Umformen der Parameterform in die Koordinatenform siehe hier.
Parallel
Vorraussetzungen:
Der Richtungsvektor der Gerade RVg und die Richtungsvektoren der Ebene RV1 und RV2 sind linear abhängig.
Wenn man 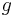 in die Koordinatenform von
in die Koordinatenform von 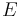 einsetzt, erhält man keine Lösung.
einsetzt, erhält man keine Lösung.
Schnittpunkt
Vorraussetzungen:
Der Richtungsvektor der Gerade RVg und die Richtungsvektoren der Ebene RV1 und RV2 sind linear unabhängig.
Wenn man 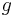 in die Koordinatenform von
in die Koordinatenform von 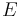 einsetzt, erhält man genau eine Lösung.
einsetzt, erhält man genau eine Lösung.
Lagebeziehungen von Ebenen und Ebenen
Zwei Ebenen können sich schneiden, zueinander parallel sein oder identisch sein. Gegeben seien die Ebene 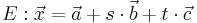 und die Ebene
und die Ebene 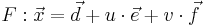
Identisch
Die Ebenen 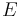 und
und 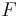 werden in die Normalenform umgewandelt. Für die Umwandlung siehe hier.
werden in die Normalenform umgewandelt. Für die Umwandlung siehe hier.
Die Normalenvektoren 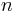 E und
E und 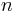 F sind linear abhängig. Der Vektor
F sind linear abhängig. Der Vektor 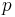 E liegt auf
E liegt auf 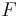 und der Vektor
und der Vektor 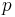 F liegt auf
F liegt auf 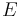 .
.

