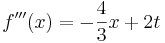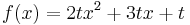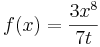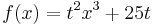Ableitung von Funktionsscharen: Unterschied zwischen den Versionen
Aus KAS-Wiki
Vieth1 (Diskussion | Beiträge) (→Beispiel zum Video) |
K (typo) |
||
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | == Besonderheiten beim Ableiten von Funktionsscharen == | ||
| + | '''Zum besseren Verständnis eignet sich auch das Video:''' | ||
| + | |||
| + | {{#ev:youtube|_ZP31iAjQ10}} | ||
| + | |||
| + | *'''Der Parameter t wird wie eine Zahl behandelt | ||
| + | ''' | ||
| + | ''-Beispiel 1:'' | ||
| + | |||
| + | <math>f\!\,(x) =2tx^2+3tx+t</math> | ||
| + | <br /> | ||
| + | ''Die Ableitung einer Zahl ist null, also ist die Ableitung von t ebenfalls null!'' | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=2t*2*x^{2-1}+3t*x^{1-1}+0</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=4t*x^1+3t*x^0</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=4tx+3t*1</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=4tx+3t</math> | ||
| + | |||
| + | |||
| + | ''-Beispiel 2:'' | ||
| + | |||
| + | <math>f\!\,(x) =\frac{3x^8}{7t}</math> | ||
| + | <br /> | ||
| + | <math>f\!\,(x)=\frac{3}{7t}*x^8</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=\frac{3}{7t}*8*x^{8-1}</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=\frac{24}{7t}x^7</math> | ||
| + | |||
| + | |||
| + | ''-Beispiel 3:'' | ||
| + | |||
| + | <math>f\!\,(x) =t^2x^3+25t</math> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=t^2*3*x^{3-1}+0</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <math>f\!\,'(x)=3t^2x^2</math> | ||
| + | |||
| + | == Beispiel zum Video == | ||
| + | |||
| + | <math>f\!\,(x) =-\frac{1}{18}x^4+\frac{t}{3}x^3</math> | ||
| + | |||
| + | |||
| + | *''Erste Ableitung'' | ||
| + | |||
| + | <math>f\!\,'(x)=-\frac{2}{9}x^3+tx^2</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | *''Zweite Ableitung'' | ||
| + | |||
| + | <math>f\!\,''(x)=-\frac{2}{3}x^2+2tx</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | *''Dritte Ableitung'' | ||
| + | |||
| + | <math>f\!\,'''(x)=-\frac{4}{3}x+2t</math> | ||
Aktuelle Version vom 17. Februar 2011, 21:28 Uhr
Besonderheiten beim Ableiten von Funktionsscharen
Zum besseren Verständnis eignet sich auch das Video:
- Der Parameter t wird wie eine Zahl behandelt
-Beispiel 1:
Die Ableitung einer Zahl ist null, also ist die Ableitung von t ebenfalls null!
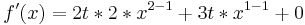
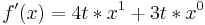
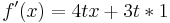
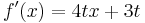
-Beispiel 2:
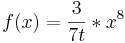
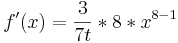
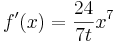
-Beispiel 3:
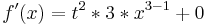
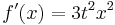
Beispiel zum Video
- Erste Ableitung
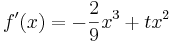
- Zweite Ableitung
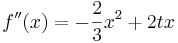
- Dritte Ableitung