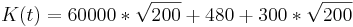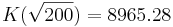Wirtschaftsbezogene Aufgaben.: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
 
(26 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 7: Zeile 7:
 
a) Bestätigen Sie, dass für die Kosten K gilt: K(t)=R(t)+60000
 
a) Bestätigen Sie, dass für die Kosten K gilt: K(t)=R(t)+60000
  
−
b) Bestimmen Sie die Funktion, die die durschnittliche jährlichen Kosten angibt. Wann sollte die Firma die Werkzeugmaschine ausmustern?
+
b) Bestimmen Sie die Funktion, die die durschnittliche jährlichen Kosten angibt. Wann sollte die Firma die Werkzeugmaschine ausmustern?'''
  
 
Lösung zu a):
 
Lösung zu a):
  
−
<math>K(t)=(480+380t)*t+60000 </math>
+
 
 +
<math>K(t)=(480+380t)*t+60000</math>
  
 
Lösung zu b)
 
Lösung zu b)
Zeile 19: Zeile 20:
 
<math>K(t)=\frac{(480+300t)*t+60000}{t} |:t      --></math>    Kosten = Gesamtreperaturkosten + Gewinn
 
<math>K(t)=\frac{(480+300t)*t+60000}{t} |:t      --></math>    Kosten = Gesamtreperaturkosten + Gewinn
  
−
<math>K(t)=\frac{(480+300t)*t+60000}{t}</math>
 
 
                
 
                
 +
<math>K(t)=\frac{ (480+300)*t+ 60000}{t^2}</math>
 +
 +
 +
<math>K(t)= 60000*t^{-1} + 480 + 300t</math>
 +
 +
 +
<math>K'(t)= -60000t^{-2} +300</math>      ----> Nach t auflösen
 +
 +
 +
<math>K'(t)=0</math>
 +
 +
 +
<math> 0 = -60000t^{-2} + 300</math>
 +
 +
<math> 60000t^{-2} = 300</math>
 +
 +
<math> 200 = t^{2}</math>
 +
 +
<math> \sqrt{200} = t</math>                    ---> Einsetzen in K (t)
  
−
<math>K(t)=\frac{ (480+300)*t+ 60000}{t<sup>Hochgestellt</sup>}</math>
+
<math> K(t)= 60000*\sqrt{200} + 480 +300 * \sqrt{200}</math>
  
−
<math>K(t)= 480+300+\frac{60000}{t}      --->      K(t)</math>   Ableiten
+
<math> K(\sqrt{200})= 8965.28</math>  
  
−
<math>K'(t)= 300+\frac{60000}{t
 
−
=== Sekundäre Überschrift ===
 
−
}</math>
 
  
  
  
 
[[Kategorie:Differential- und Integralrechnung]]
 
[[Kategorie:Differential- und Integralrechnung]]

Aktuelle Version vom 10. Februar 2011, 11:02 Uhr

Seite 56 Aufgabe 6

Vor fünf Jahren hat eine Firma eine Werkzeugmaschine zum Preis von 60000€ gekauft. Statistische Daten sprechen für Gesamtreperaturkosten R mit der Geleichung: R(t)=(480+300t)*t mit t in Jahren, R(t) in €

a) Bestätigen Sie, dass für die Kosten K gilt: K(t)=R(t)+60000

b) Bestimmen Sie die Funktion, die die durschnittliche jährlichen Kosten angibt. Wann sollte die Firma die Werkzeugmaschine ausmustern?

Lösung zu a):


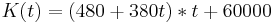
K(t)=(480+380t)*t+60000

Lösung zu b)


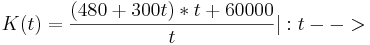K(t)=\frac{(480+300t)*t+60000}{t} |:t --> Kosten = Gesamtreperaturkosten + Gewinn


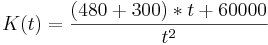
K(t)=\frac{ (480+300)*t+ 60000}{t^2}


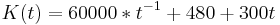
K(t)= 60000*t^{-1} + 480 + 300t


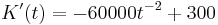K'(t)= -60000t^{-2} +300 ----> Nach t auflösen


K'(t)=0


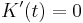
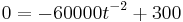
0 = -60000t^{-2} + 300

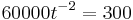
60000t^{-2} = 300

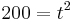
200 = t^{2}

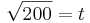\sqrt{200} = t ---> Einsetzen in K (t)

K(t)= 60000*\sqrt{200} + 480 +300 * \sqrt{200}

K(\sqrt{200})= 8965.28

Von „http://kas.zum.de/index.php?title=Wirtschaftsbezogene_Aufgaben.&oldid=5359“