Funktionenscharen.: Unterschied zwischen den Versionen
Aus KAS-Wiki
Negin1 (Diskussion | Beiträge) |
Vieth1 (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
| <math>\!Extremstellen</math> | | <math>\!Extremstellen</math> | ||
| <math>\!f'(x)=0, pq-Formel, Polynomdivision</math> | | <math>\!f'(x)=0, pq-Formel, Polynomdivision</math> | ||
| + | {{#ev:youtube|iWl6s9baQk0}} | ||
| <math>\!f''(x)> 0 </math> »Minimum; <math>\!f''(x)<0 </math> » Maximum, <math>\!f''(x)</math> ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist <math>\!f''(x)</math> abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt. | | <math>\!f''(x)> 0 </math> »Minimum; <math>\!f''(x)<0 </math> » Maximum, <math>\!f''(x)</math> ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist <math>\!f''(x)</math> abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt. | ||
|- | |- | ||
| Zeile 19: | Zeile 20: | ||
| <math>\!Symmetrie(Punkt-,Achsen-)</math> | | <math>\!Symmetrie(Punkt-,Achsen-)</math> | ||
| <math>\!Punktsymmetrie: -f(x)=f(-x); Achsensymmetrie: f(x)=f(-x)</math> | | <math>\!Punktsymmetrie: -f(x)=f(-x); Achsensymmetrie: f(x)=f(-x)</math> | ||
| + | {{#ev:youtube|m-r8Mjyxl0s}} | ||
| Bei ganzrationalen Funktionen <math>\!(ax^3+bx^2+cx+d)</math>: Achsensymmetrie: Nur gerade Exponenten; Punktsymmetrie: Nur ungerade Exponenten und muss durch (0|0) gehen. | | Bei ganzrationalen Funktionen <math>\!(ax^3+bx^2+cx+d)</math>: Achsensymmetrie: Nur gerade Exponenten; Punktsymmetrie: Nur ungerade Exponenten und muss durch (0|0) gehen. | ||
|- | |- | ||
| <math>\!Gemeinsame Punkte</math> | | <math>\!Gemeinsame Punkte</math> | ||
| t1 und t2 mit t1 ≠ t2 einsetzen und dann gleichsetzen | | t1 und t2 mit t1 ≠ t2 einsetzen und dann gleichsetzen | ||
| + | {{#ev:youtube|1HZxJnJPrjs}} | ||
| t1 ≠ t2 <math>\!f</math> | | t1 ≠ t2 <math>\!f</math> | ||
|- | |- | ||
| Zeile 29: | Zeile 32: | ||
| <math>\! \frac{-1}{x^2*ln\ a}</math> | | <math>\! \frac{-1}{x^2*ln\ a}</math> | ||
|- | |- | ||
| − | | | + | | Ortskurve der Extremstellen/Wendestellen |
| 1. Bestimmung der Extremstelle x, 2.Extremstelle in ft(x) einsetzen » nach y auflösen, Diex-Koordinate nach t auflösen und t in y-Koordinate einsetzen | | 1. Bestimmung der Extremstelle x, 2.Extremstelle in ft(x) einsetzen » nach y auflösen, Diex-Koordinate nach t auflösen und t in y-Koordinate einsetzen | ||
| + | {{#ev:youtube|Sb105uCtI8s}} | ||
| Geht nur, wenn Extremstelle von x abhängig ist ! | | Geht nur, wenn Extremstelle von x abhängig ist ! | ||
|- | |- | ||
Aktuelle Version vom 17. Februar 2011, 13:37 Uhr
|
|
|
|---|---|---|
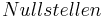
|
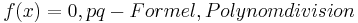
|
Ist die Nullstelle von t abhängig? Ja » Einschränkungen bezüglich t beachten: » Habe ich durch t dividiert ? » Habe ich die Wurzel aus t gezogen ? |
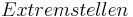
|
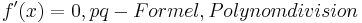
|
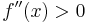 »Minimum; »Minimum; 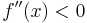 » Maximum, » Maximum, 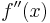 ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist ≠ 0, sonst Sattelpunkt. Ist die Extremstelle von t abhängig ? Ja » Abgleich von t mit der Aufgabenstellung (Einschränkungen für t) » ist 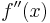 abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt. abhängig von t ? »» Dann Falluntersuchung ob ein Minimum oder Maximum vorliegt.
|
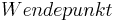
|
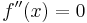 , pq-Formel; Polynomdivision , pq-Formel; Polynomdivision
|
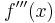 ≠ 0 sonst Ø Wendepunkt. Ist die Wendestelle von t abhängig ? »Ja wenn ... ≠ 0 sonst Ø Wendepunkt. Ist die Wendestelle von t abhängig ? »Ja wenn ...
|
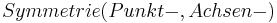
|
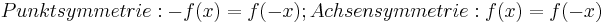
|
0) gehen. |
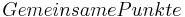
|
t1 und t2 mit t1 ≠ t2 einsetzen und dann gleichsetzen | t1 ≠ t2 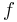
|
|
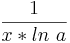
|
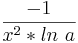
|
| Ortskurve der Extremstellen/Wendestellen | 1. Bestimmung der Extremstelle x, 2.Extremstelle in ft(x) einsetzen » nach y auflösen, Diex-Koordinate nach t auflösen und t in y-Koordinate einsetzen | Geht nur, wenn Extremstelle von x abhängig ist ! |

