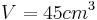Geometrieaufgabe.: Unterschied zwischen den Versionen
Daryna (Diskussion | Beiträge) |
Daryna (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 47: | Zeile 47: | ||
O(c)= 2*5*<math>\frac{9}{c}</math> + 2*5*c + 2*<math>\frac{9}{c}</math>*c | O(c)= 2*5*<math>\frac{9}{c}</math> + 2*5*c + 2*<math>\frac{9}{c}</math>*c | ||
| − | + | ||
| + | = <math>\frac{90}{c}</math> + 10c + 18 | ||
1.Ableitung erstellen: | 1.Ableitung erstellen: | ||
| − | O'(c)= - <math>\frac{90}{ | + | O'(c) = - <math>\frac{90}{c^2}</math>+ 10 |
| + | |||
| + | 0 = - <math>\frac{90}{c^2}</math>+ 10 | - 10 | ||
| + | |||
| + | -10 = - <math>\frac{90}{c^2}</math> | <math>*c^2</math> | ||
| + | |||
| + | <math>-10*c^2</math>= - 90 | : -10 | ||
| + | |||
| + | <math>c^2</math> = 9 | +/- <math>\sqrt{}</math> | ||
| + | |||
| + | |||
| + | c1= 3 c2= -3 | ||
| + | |||
| + | 2.Ableitung erstellen: | ||
| + | |||
| + | O"(c) = <math>\frac{180}{c^3}</math> | ||
| + | |||
| + | c1 und c2 einsetzten und nach Tiefpunkt suchen: | ||
| + | |||
| + | O"(3) > 0 daraus folgt, dass ein TP vorliegt -> minimale Oberfläche | ||
| + | |||
| + | c= 3 in Zielfunktion einsetzen: | ||
| + | |||
| + | 45 = 5*b*c | ||
| + | 45 = 5*b*3 | : 15 | ||
| + | 3 = b | ||
| + | |||
| + | |||
| + | <u>Ergebnis:</u> | ||
| + | |||
| + | a=5 b=3 c=3 für Volumen <math>V=45cm^3</math> | ||
| − | |||
Aktuelle Version vom 15. Februar 2011, 13:11 Uhr
 Aufgabe
Eine Zündholzschachtel soll 5 cm lang sein und das Volumen 45 cm³ haben. Bei welcher Breite und Höhe braucht man zur Herstellung am wenigsten Material? Bei der Lösung der Aufgabe werden überlappende Flächen nicht weiter beachtet! |
Hilfsmittel zur Lösung der Problematik:
Volumen vom Quader = a*b*c
Oberflächeninhalt = 2ab+2ac+2bc
Nebendingungen aufstellen:
1.NB:
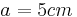
2.NB:
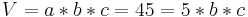
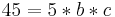
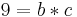
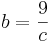
Zielfunktion aufstellen:
b in Oberflächenformel einsetzen
O=2*5*b+2*5*c+2*b*c
2.NB nach einer Variable auflösen, um später in die Zielfunktion einsetzen zu können.
45=5*b*c
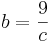
Beide NB. in die Zielfunktion einsetzen um nur noch eine Variable zu erhalten:
O(c)= 2*5*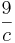
+ 2*5*c + 2*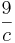*c
= 
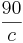+ 10c + 18
1.Ableitung erstellen:
O'(c) = -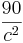 
+ 10
0 = - 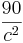+ 10 | - 10
-10 = - |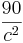 
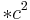
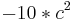= - 90 | : -10
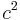= 9 | +/-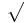 
c1= 3 c2= -3
2.Ableitung erstellen:
O"(c) =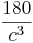 
c1 und c2 einsetzten und nach Tiefpunkt suchen:
O"(3) > 0 daraus folgt, dass ein TP vorliegt -> minimale Oberfläche
c= 3 in Zielfunktion einsetzen:
45 = 5*b*c 45 = 5*b*3 | : 15 3 = b
Ergebnis:
a=5 b=3 c=3 für Volumen 
