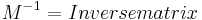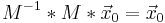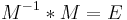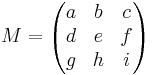Prozeß- und Übergangsmatizen: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 9: | Zeile 9: | ||
Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen. | Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen. | ||
| − | === Einheitsmatrix === | + | === Einheitsmatrix: === |
<math> E*\vec a=\vec a </math> | <math> E*\vec a=\vec a </math> | ||
| − | <math> M^n=M </math> | + | <math> \!M^n=M </math> |
Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen. | Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen. | ||
| + | === Addition von Matrizen: === | ||
<math>A+B= \begin{pmatrix} a_1 & a_2 \\ a_3 & a_4 \end{pmatrix}+\begin{pmatrix} b_1 & b_2 \\ b_3 & b_4 \end{pmatrix}=\begin{pmatrix} a_1+b_1 & a_2+b_2 \\ a_3+b_3 & a_4+b_4 \end{pmatrix} </math> | <math>A+B= \begin{pmatrix} a_1 & a_2 \\ a_3 & a_4 \end{pmatrix}+\begin{pmatrix} b_1 & b_2 \\ b_3 & b_4 \end{pmatrix}=\begin{pmatrix} a_1+b_1 & a_2+b_2 \\ a_3+b_3 & a_4+b_4 \end{pmatrix} </math> | ||
| + | |||
| + | === Inverse: === | ||
| + | |||
| + | <math>\!M^{-1}= Inversematrix</math> | ||
| + | |||
| + | <math>M^{-1}*M* \vec x_0= \vec x_0</math> | ||
| + | |||
| + | <math>\!M^{-1}*M=E</math> | ||
| + | |||
| + | <math>M=\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}</math> | ||
Version vom 1. Dezember 2009, 12:41 Uhr
Eine Übergangsmatrix beschreibt einen Übergang von einer Dimension in eine andere.
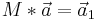
Inhaltsverzeichnis |
Grenzwert:
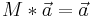
Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen.
Einheitsmatrix:
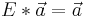
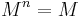
Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen.
Addition von Matrizen:
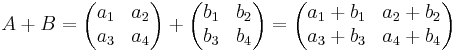
Inverse: