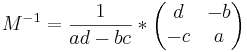Prozeß- und Übergangsmatizen
Inhaltsverzeichnis[Verbergen] |
Übergangsmatrizen:
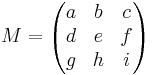
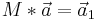
Eine Übergangsmatrix beschreibt einen Übergang von einer Dimension in eine andere.
Addition von Matrizen:
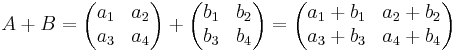
Multiplikation:
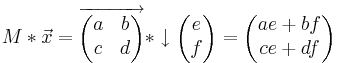
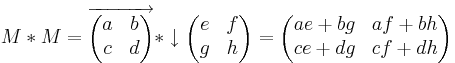
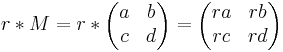
Inverse:
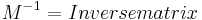
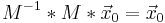
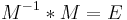
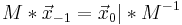
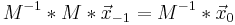
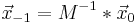
Die inverse Matrix stellt den vorherigen Zustand dar.
Das LGS darf nur eine Lösung besitzen, sonst ist keine inverse Matrix möglich.
Die Matrix multipliziert mit der inversen Matrix ergibt den Eigenvektor.
Grenzwert:
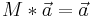
Ein Grenzwert ist dann erreicht, wenn sich die Matrix durch einen Vektor nicht mehr ändert z.B. bei Populationsentwicklungen.
Wenn ein Grenzwert existiert, sind alle Spalten gleich, eine Gleichgewichtsverteilung besteht.
Einheitsmatrix:
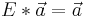
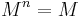
Nach n Jahren tritt wieder der gleiche Zustand ein, ist also zyklisch, wie bei Tierpopulationen.
Übergangsgraph:
Determinanten:
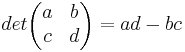
Eine Determinante beschreibt den Übergang von einer Matrix (M) zu einer inversen Matrix (M^-1).
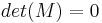 ->dann existiert keine inverse Matrix!
->dann existiert keine inverse Matrix!
Wenn die 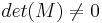 , dann heißt die Matrix affine Abbildung!
, dann heißt die Matrix affine Abbildung!