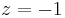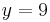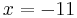Lösung linearer Gleichungssysteme: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 1: | Zeile 1: | ||
=== Gaußches Eliminierungsverfahren === | === Gaußches Eliminierungsverfahren === | ||
| + | |||
| + | Die Operationen: | ||
| + | - Multiplikation einer Gleichung mit einem Faktor | ||
| + | - Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung | ||
| + | |||
Aufstellen des linearen Gleichungssystems. | Aufstellen des linearen Gleichungssystems. | ||
| − | <math>\!1x +2y +3z = 4</math> <math>\! | + | '''I''' |
| + | |||
| + | <math>\!4 = 1x +2y +3z </math> | ||
| + | |||
| + | '''II''' | ||
| + | |||
| + | <math>\! 1 = 2x +3y +4z </math> | ||
| + | |||
| + | '''III''' | ||
| + | |||
| + | <math>\! 2 = 3x +4y +1z </math> | ||
| + | |||
| + | |||
| + | Durch das Subtraktionsverfahren eliminiert man <math>\!x</math> aus 2 Gleichungen | ||
| + | |||
| + | |||
| + | |||
| + | '''I''' | ||
| + | |||
| + | <math>\! 4 = 1x +2y +3z </math> | ||
| + | |||
| + | '''I*2 - II''' | ||
| + | |||
| + | <math>\! 7 = 1y +2z</math> | ||
| + | |||
| + | '''III''' | ||
| + | |||
| + | <math>\! 2 = 3x +4y +1z </math> | ||
| + | |||
| + | |||
| + | |||
| + | '''I''' | ||
| + | |||
| + | <math>\! 4 = 1x +2y +3z </math> | ||
| + | |||
| + | '''I*2 - II''' | ||
| + | |||
| + | <math>\! 7 = 1y +2z</math> | ||
| + | |||
| + | '''I*3 - III''' | ||
| + | |||
| + | <math>\! 10 = 2y +8z </math> | ||
| + | |||
| + | |||
| + | Durch erneute Subtraktion wird <math>\!Y</math> eliminiert. | ||
| + | |||
| + | '''I''' | ||
| + | |||
| + | <math>\! 4 = 1x +2y +3z </math> | ||
| + | |||
| + | '''I*2 -II''' | ||
| + | |||
| + | <math>\! 7 = 1y +2z</math> | ||
| + | |||
| + | '''II*2 - III''' | ||
| + | |||
| + | <math>\! 4 = -4z </math> | ||
| + | |||
| + | |||
| + | Durch Einsetzten und Lösen erhält man: | ||
| + | |||
| + | |||
| + | <math>\! z = -1 </math> | ||
| − | <math>\! | + | <math>\! y = 9 </math> |
| − | <math>\! | + | <math>\! x = -11 </math> |
Version vom 7. Dezember 2009, 10:43 Uhr
Gaußches Eliminierungsverfahren
Die Operationen: - Multiplikation einer Gleichung mit einem Faktor - Addition/Subtraktion des Vielfachen einer Gleichung mit einer anderen Gleichung
Aufstellen des linearen Gleichungssystems.
I
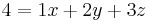
II
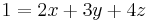
III
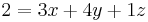
Durch das Subtraktionsverfahren eliminiert man 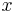 aus 2 Gleichungen
aus 2 Gleichungen
I
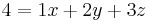
I*2 - II
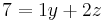
III
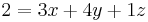
I
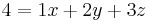
I*2 - II
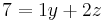
I*3 - III
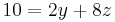
Durch erneute Subtraktion wird 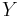 eliminiert.
eliminiert.
I
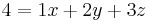
I*2 -II
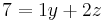
II*2 - III
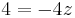
Durch Einsetzten und Lösen erhält man: