Rotationsintegrale: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 6: | Zeile 6: | ||
<math>V(x)=\pi*\int_a^b(f(x))^2dx</math> | <math>V(x)=\pi*\int_a^b(f(x))^2dx</math> | ||
| − | Volumen des Körpers bei Rotation der Flachen zwischen dem Graphen von f und der y-Achse im Intervall[a;b]. Dabei sei f umkehrbar mit x= | + | Volumen des Körpers bei Rotation der Flachen zwischen dem Graphen von f und der y-Achse im Intervall[a;b]. Dabei sei f umkehrbar mit x=f^-1(y) |
Version vom 1. Dezember 2009, 13:12 Uhr
Rotationsintegral(Volumen von Rotationskörpern)
Volumen des Körpers bei Rotation der Flächen zwischen dem Graphen von f und der x-Achse im Intervall [a;b].
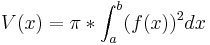
Volumen des Körpers bei Rotation der Flachen zwischen dem Graphen von f und der y-Achse im Intervall[a;b]. Dabei sei f umkehrbar mit x=f^-1(y)

