Rotationsintegrale: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
Zeile 25: Zeile 25:
  
 
<math>=\pi*[\frac 1{12}x^3+x]^4_0</math>
 
<math>=\pi*[\frac 1{12}x^3+x]^4_0</math>
 +
 +
Das führt zu folgendem Ergebnis:
 +
 +
<math>\frac {28}3*\pi\approx 29,32</math>
 +
 +
Der Graph würde folgendermaßen aussehen:

Version vom 1. Dezember 2009, 13:15 Uhr

Rotationsintegral(Volumen von Rotationskörpern)

Das Volumen des Körpers bei der Rotation der Flächen zwischen dem Graphen von f und der x-Achse im Intervall [a;b].

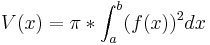
V(x)=\pi*\int_a^b(f(x))^2dx

Das Volumen des Körpers bei der Rotation der Flächen zwischen dem Graphen von f und der y-Achse im Intervall[a;b]. Dabei sei f umkehrbar mit 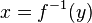x=f^{-1}(y).

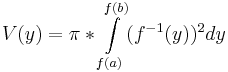
V(y)=\pi*\int\limits_{f(a)}^{f(b)}(f^{-1}(y))^2dy


Anwendung am Beispiel

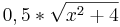0,5*\sqrt{x^2+4} im Intervall [0;4].

Gesucht ist das Volumen der Funktion f(x) rotiert um die x-Achse.

Dazu setzt man die Werte in die Formel 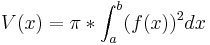V(x)=\pi*\int_a^b(f(x))^2dx ein.

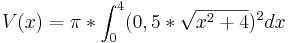
V(x)=\pi*\int_0^4(0,5*\sqrt{x^2+4})^2dx

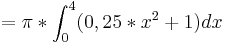
=\pi*\int_0^4(0,25*{x^2+1})dx

=\pi*[\frac 1{12}x^3+x]^4_0

Das führt zu folgendem Ergebnis:

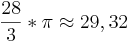
\frac {28}3*\pi\approx 29,32

Der Graph würde folgendermaßen aussehen:

Von „http://kas.zum.de/index.php?title=Rotationsintegrale&oldid=281“