Exponentialfunktionen.: Unterschied zwischen den Versionen

Version vom 17. Dezember 2010, 10:29 Uhr

> Eigenschaften der Funktion:

Die Funktionsgleichung der Exponentialfunktion besteht aus folgender Form:

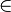
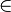
                 f(x) = a^x        oder auch        g(x) = ca^x    wobei: c  ,    a > 0,    x    ist.

Die Exponentialfunktion beschreibt für a > 1 einen Wachstumsprozess und für 0 < a < 1 einen Zerfallsprozess.

D.h.: a > 1 hat die Eigenschaft STRENG MONOTON STEIGERND und 0 < a < 1 hat die Eigenschaft STRENG MONOTON FALLEND.

> Die natürliche Exponentialfunktion und ihre Ableitung:

Die natürliche Exponentialfunktion f mit f(x)= e^x hat die Ableitungsfunktion f ´mit f ´(x)= e^x. Eine Stammfunktion ist F mit F(x)= e^x.

ALLGEMEIN:

Ableitung:
f (x) = e^{v (x)}

f ´(x)= e^{v (x)} $\cdot$ v ´ (x)

Stammfunktion:
F(x) = 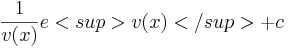$\frac{1}{v´(x)}e<sup>v (x)</sup>+c$

BEISPIELE:
1.) f (x) = e^5x

f ´(x)= 5 e^5x

F(x)= $\frac{1}{5}$ e^5x+c

2.) f(x)=5 e ^3x+7

f ´(x)= 5 e^3x+7 $\cdot$ 3 = 15 e^3x+7

F(x) = $\frac{5}{3}$ e^3x+7

> Ableitung und Integrieren zusammengesetzter Funktionen:

> Untersuchung von Exponentialfunktionen: > Kurvendiskussion Anhand eines Beispieles:

Funktion: f(x)= 5x $\cdot$ e^{- 1/2x}

1.) Ableitungen:
f ' (x)= 5 $\cdot$ e^{- 1/2x} + 5x $\cdot$ e^{- 1/2x} $\cdot$ ( - 1/2)
= e^{- 1/2x} (5 - 5/2x)

f ' '(x)= - 1/2e^{- 1/2x} (5 - 5/2x) + e^{- 1/2x} $\cdot$ (- 5/2)
= e^{- 1/2x} (- 5/2 + 5/4x - 5/2)
= e^{- 1/2x} (5/4x - 5)

f ' ' '(x)= - 1/2e^{- 1/2x} (5/4x - 5) + e^{- 1/2x} $\cdot$ 5/4
= e^{- 1/2x} (- 5/8x + 5/2 + 5/4)
= e^{- 1/2x} (15/4 - 5/8x)

2.) Symmetrie:
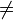f ( -x) = 5 $\cdot$ (-x) $\cdot$ e^{- 1/2(-x)} = - 5x $\cdot$ e^1/2x $\ne$ f (x) --> KEINE ACHSENSYMMETRIE
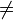f ( -x) = - 5x $\cdot$ e^1/2x $\ne$ - f(x) --> KEINE PUNKTSYMMETRIE

3.) Nullstellen:
notw. Bedingung f (x) = 0
5x $\cdot$ e^{- 1/2x} = 0
x = 0
N(0/0)

4.) Verhalten gegen 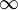$\infty$ :
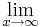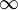$\lim_{x \to \infty}$ 5x $\cdot$ e^{- 1/2x} = 0 , weil 5x $\to$ $\infty$ und e^{- 1/2x} $\to$ 0

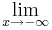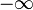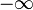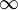
$\lim_{x \to -\infty}$ 5x $\cdot$ e^{- 1/2x} = $- \infty$ , weil 5x $\to$ $- \infty$ und e^{- 1/2x} $\to$ $\infty$

5. Extremwerte:
notw. Bedingung f ' (x) = 0
e^{- 1/2x} $\cdot$ (5- 5/2x) = 0
Da e^{- 1/2x} > 0 ist, braucht man nur die Klammer zu betrachten.
5 - 5/2x = 0
x = 2

hinreichende Bedingung f ' ' (2), um zu überprüfen, ob es Hoch bzw Tiefpunkte gibt:
f' '(2) = e^{- 1/22}(5/4 $\cdot$ 2 - 5)
= e^{- 1}( 5/2 - 5)
= - 0,92 < 0 daraus folgt: Es sind Hochpunkte vorhanden
f (2) einsetzen, um zu überprüfen, wo der Hochpunkt ist
f (2) = 5 $\cdot$ 2 $\cdot$ e^{- 1/22}

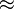$\approx$ 3,68 d.h.: Hochpunkt (2 / 3,68)

6. Wendestellen:
notw. Bedingung f ' ' (x) = 0
e^{- 1/2x}( 5/4x -5) = 0
5/4x -5 = 0
x = 4

hinreichende Bedingung: f ' ' '(4) um zu überprüfen, ob es Wendestellen gibt:
e^{- 1/24}( 15/4 - 5/8 $\cdot$ 4)
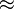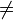$\approx$ 0,17 $\ne$ 0 d.h.: Wendestelle vorhanden
bei: f (4)= 5 $\cdot$ 4 $\cdot$ e^{- 1/24}
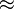$\approx$ 2,17 d.h.: Wendestelle (4/ 2,71)

7. Graph:

@@ Zeile 19: / Zeile 19: @@
 f ´(x)= e<sup>v (x)</sup><math>\cdot</math> v ´ (x)
-Stammfunktion:<br /> F(x) = <math>\frac{1}{v´(x)}</math>e<sup>v (x)</sup>+c
+Stammfunktion:<br /> F(x) = <math> \frac{1}{v´(x)}e<sup>v (x)</sup>+c </math>
 BEISPIELE: <br /> 1.) f (x) = e<sup>5x</sup><br /><br />f ´(x)= 5 e<sup>5x</sup><br /><br />F(x)= <math>\frac{1}{5}</math> e<sup>5x</sup>+c<br /> <br />2.) f(x)=5 e <sup>3x+7</sup><br /><br />f ´(x)= 5 e<sup>3x+7</sup><math>\cdot</math>3 = 15 e<sup>3x+7</sup><br /><br /> F(x) =<math>\frac{5}{3}</math> e<sup>3x+7</sup>

Exponentialfunktionen.: Unterschied zwischen den Versionen

Version vom 17. Dezember 2010, 10:29 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge