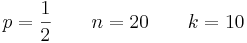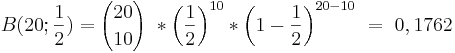Binominalverteilung.: Unterschied zwischen den Versionen
Aus KAS-Wiki
| Zeile 20: | Zeile 20: | ||
<math> | <math> | ||
| − | B(20;\frac{1}{2}) = {20 \choose 10}\ * (\frac{1}{2}) ^{10} * (1- \frac{1}{2} )^{20-10} \ = \ 0,1762 | + | B(20;\frac{1}{2}) = {20 \choose 10}\ * \left (\frac{1}{2} \right ) ^{10} * \left (1- \frac{1}{2} \right )^{20-10} \ = \ 0,1762 |
</math> | </math> | ||
Version vom 17. Dezember 2010, 12:17 Uhr
Formel zu Berechnung der Binominalverteilung:
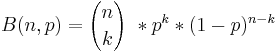
B = Die Wahrscheinlichkeit k Erfolge aus n Versuchen zu bekommen
p = Wahrscheinlichkeit für den Treffer
n = Gesamtzahl der durchgeführten Versuche
k = Anzahl der günstigen Ereignisse/Treffer
Beispielrechnung: