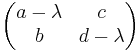Eigenwerte und Eigenvektoren (Fixelemente).: Unterschied zwischen den Versionen

Aus KAS-Wiki
Wechseln zu: Navigation, Suche
(→‎Bestimmung von Eigenvektoren)
(→‎Beispielaufgaben)
Zeile 28: Zeile 28:
  
 
== Beispielaufgaben ==
 
== Beispielaufgaben ==
 +
A=<math>\begin{pmatrix}
 +
4 & 1 \\
 +
-1 & 2
 +
\end{pmatrix}</math>
 +
 +
Aufstellen der charakteristischen Gleichung:
 +
                                            (4-<math>\lambda</math>)(2-<math>\lambda</math>)+1=0'''
 +
                                            <=><math>\lambda</math><sup>2</sup>-6<math>\lambda</math>+8+1=0
 +
                                            <=><math>\lambda</math><sup>2</sup>-6<math>\lambda</math>+9=0
 +
                                            <=><math>\lambda</math><sub>1/2</sub>=3<math>\pm</math><math>\wurzel{9-9}</math>

Version vom 8. Dezember 2009, 14:25 Uhr

Inhaltsverzeichnis

 [Verbergen] 

Definition

Eigenwerte

Eigenvektoren

Bestimmung von Eigenwerten

Gegeben ist die Abbildungsmatrix A=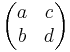\begin{pmatrix} a & c\\ b & d \end{pmatrix}.

Aufstellen der charakteristischen Gleichung: 

                     det(A-\lambdaA)=0<=>(a-\lambda)(d-\lambda)-bc=0

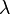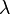Die Lösungen \lambda1/\lambda2 dieser Gleichung sind die Eigenwerte. Die charakteristische Gleichung hat eine, zwei oder keine Lösung.

Bestimmung von Eigenvektoren 

Die Eigenvektoren erhält man, indem man das LGS \begin{pmatrix}
a-\lambda & c \\
b & d-\lambda
\end{pmatrix} \vec x=\vec0 löst.

Für den Eigenwert 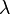\lambda=1 erhält man eine Fixpunktgerade, für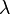 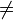\lambda\ne1 eine Fixgerade.

Beispielaufgaben 

A=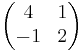\begin{pmatrix}
4 & 1 \\
-1 & 2
\end{pmatrix}

Aufstellen der charakteristischen Gleichung: 

                                           (4-\lambda)(2-\lambda)+1=0
                                           <=>\lambda2-6\lambda+8+1=0
                                           <=>\lambda2-6\lambda+9=0
                                           <=>\lambda1/2=3\pmFehler beim Parsen(Unbekannte Funktion „\wurzel“): \wurzel{9-9}
Von „http://kas.zum.de/index.php?title=Eigenwerte_und_Eigenvektoren_(Fixelemente).&oldid=700“